题目内容

【解析】解析:(1) .由题意
.由题意 ,即
,即
 ,∴
,∴ ,
,
∵ 且
且 ,∴数列
,∴数列 是以
是以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,

以上各式两边分别相加得 ,∴
,∴ ,
,
当 时,上式也成立,∴
时,上式也成立,∴
(2)当 时,
时,


由 ,得
,得 ,
, ,
,
当 时
时 ,当
,当 时
时 ,
,
因此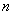 的最
的最 小值为
小值为 .
.
(3)∵
令 ,则有:
,则有:
则

 ,
,
即存在函数 满足条件.
满足条件.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
题目内容

【解析】解析:(1) .由题意
.由题意 ,即
,即
 ,∴
,∴ ,
,
∵ 且
且 ,∴数列
,∴数列 是以
是以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,

以上各式两边分别相加得 ,∴
,∴ ,
,
当 时,上式也成立,∴
时,上式也成立,∴
(2)当 时,
时,


由 ,得
,得 ,
, ,
,
当 时
时 ,当
,当 时
时 ,
,
因此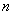 的最
的最 小值为
小值为 .
.
(3)∵
令 ,则有:
,则有:
则

 ,
,
即存在函数 满足条件.
满足条件.

 智慧小复习系列答案
智慧小复习系列答案