题目内容
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,写出
时,写出![]() 的单调递增区间(不需写出推证过程);
的单调递增区间(不需写出推证过程);
(2)当![]() 时,若直线
时,若直线![]() 与函数
与函数![]() 的图象相交于
的图象相交于![]() 两点,记
两点,记![]() ,求
,求![]() 的最大值;
的最大值;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)4;(3)
;(2)4;(3)![]()
【解析】
(1)当![]() 时,
时,![]() ,由此能求出
,由此能求出![]() 的单调递增区间;
的单调递增区间;
(2)由![]() ,得当
,得当![]() 时,
时,![]() 的图象与直线
的图象与直线![]() 没有交点;当
没有交点;当![]()
![]() 或
或![]() 时,y=f(x)
时,y=f(x)![]() 的图象与直线
的图象与直线![]() 只有一个交点;当
只有一个交点;当![]() 时,
时,![]() ;当
;当![]() 时,由
时,由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,由此能求出
,由此能求出![]() 的最大值;
的最大值;
(3)要使关于x的方程![]() 有两个不同的实数根
有两个不同的实数根![]() ,则
,则![]() ,且
,且![]() ,根据
,根据![]() ,且
,且![]() 进行分类讨论能求出
进行分类讨论能求出![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]()
在![]() 和
和![]() 单调递增
单调递增
(2)因为x>0,所以
(ⅰ)当a>4时,![]() ,函数的
,函数的![]() ,
,
![]() 函数的图像与直线y=4没有交点;
函数的图像与直线y=4没有交点;
(ⅱ)当a=4时,![]() ,函数的最小值是4,
,函数的最小值是4,
![]() 的图象与直线
的图象与直线![]() 只有一个交点;
只有一个交点;
当![]() 时,
时,![]()
![]() 与
与![]() 有1个交点,交点坐标
有1个交点,交点坐标![]() ,不满足条件;
,不满足条件;
(ⅲ)当0<a<4时,![]()
即![]()
![]()
![]() ,
,
![]() ,
,
![]() ;
;
(ⅳ)当a<0时,如图:
由![]()
![]()
得![]() ,
,
解得![]() ;
;
由![]() ,
,![]()
得![]()
解得![]() .
.
所以![]() .
.
综上:![]() 的最大值是4.
的最大值是4.
(Ⅲ)要使关于![]() 的方程
的方程![]() (*)
(*)
当![]() 时,去绝对值得
时,去绝对值得![]() ,解得
,解得![]() ,不成立,舍;
,不成立,舍;
当![]() 时,去绝对值
时,去绝对值![]() ,
,![]()
化简为:![]() ,
,![]() 不成立,舍;
不成立,舍;
当![]() 时,
时,![]() ,
,![]() ,也不成立,舍;
,也不成立,舍;
![]()
![]() .
.
(ⅰ)当![]() 时,由(*)得
时,由(*)得![]() ,
,
所以![]() ,不符合题意;
,不符合题意;
(ⅱ)当![]() 时,由(*)得
时,由(*)得![]() ,其对称轴
,其对称轴![]() ,不符合题意;
,不符合题意;
(ⅲ)当![]() ,且
,且![]() 时,
时,
当![]() 时,
时,![]() ,
,![]() ,
,
整理为:![]() ,
,![]() 不成立,
不成立,
当![]() 时,
时,
要使直线![]() 与函数
与函数![]() 图像在
图像在![]() 内有两个交点,
内有两个交点,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,
只需满足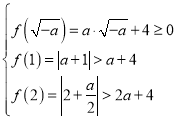
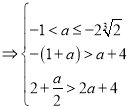 ,
,
解得:![]() ;①
;①
当![]() 时
时
![]() ,
,
整理得:![]() ,
,
若在区间![]() 方程有2个不等实数根,只需满足
方程有2个不等实数根,只需满足
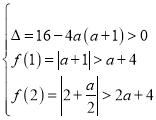
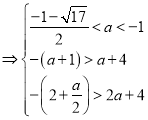 ,
,
解得:![]() ②,
②,
综上①②可知,![]() 的范围是
的范围是![]()
综上所述,a的取值范围为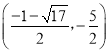 .
.

练习册系列答案
相关题目