题目内容
如图,在四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,点
,点 分别为
分别为 的中点,且
的中点,且 ,
, ,
, .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.

解:(Ⅰ)证明:取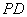 中点
中点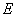 ,连结
,连结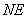 ,
,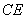 .
.
 为
为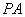 中点,
中点,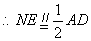 ,
,
又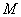 为
为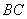 中点,底面
中点,底面 为平行四边形,
为平行四边形,
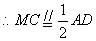 .
.
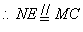 ,即
,即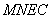 为平行四边形,
为平行四边形,
∴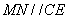
 平面
平面 ,且
,且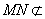 平面
平面 ,
,
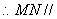 平面
平面 . ……………………………………………6分
. ……………………………………………6分
(其它证法酌情给分)
(Ⅱ)方法一:
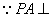 平面
平面 ,
,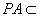 平面
平面 ,
, 平面
平面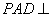 平面
平面 ,
,
过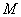 作
作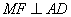 ,则
,则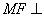 平面
平面 ,连结
,连结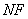 .
.
则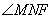 为直线
为直线 与平面
与平面 所成的角,
所成的角,
由 ,
, ,
,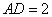 ,得
,得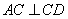 ,
,
由 ,得
,得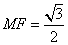 ,
,
在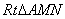 中,
中,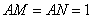 ,得
,得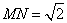 .
.
在 中,
中, ,
,
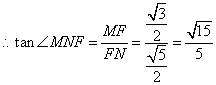 ,
,
直线 与平面
与平面 所成角的正切值为
所成角的正切值为 . ……………………12分
. ……………………12分
方法二:
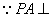 平面
平面 ,
,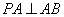 ,
,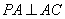 ,
,
又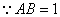 ,
, ,
,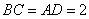 ,
,
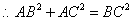 ,
,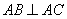 .
.
 如图,分别以
如图,分别以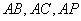 为
为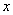 轴,
轴,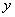 轴,
轴,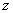 轴,
轴,
建立空间直角坐标系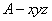 ,
,
则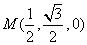 ,
,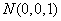 ,
,
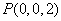 ,
,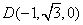 ,
,
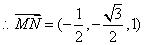 ,
,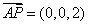 ,
,
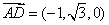 ,
,
设平面 的一个法向量为
的一个法向量为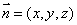 ,则
,则
由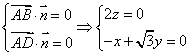 ,令
,令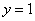 得
得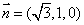 ,
,
设 与平面
与平面 所成的角为
所成的角为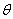 ,则
,则
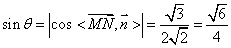
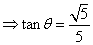 ,
,
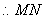 与平面
与平面 所成角的正切值为
所成角的正切值为 .………………………12分
.………………………12分

练习册系列答案
相关题目
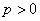 ,抛物线方程为
,抛物线方程为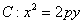 .如图所示,过焦点
.如图所示,过焦点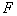 作
作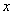 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为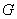 ,已知抛物线在点
,已知抛物线在点 .
.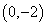 作抛物线
作抛物线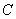 的切线,若切点在第二象限,求切线
的切线,若切点在第二象限,求切线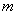 的方程;
的方程;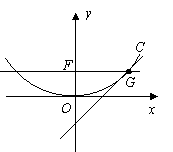

 的焦点F的直线依次交拋物线及准线于点A,B,C,
的焦点F的直线依次交拋物线及准线于点A,B,C,
 B
B  C.
C. D.
D.

 的图象,只需要将函数
的图象,只需要将函数 的图象 ( )
的图象 ( ) 个单位 B.向右平移
个单位 B.向右平移

 的公差
的公差 ,首项
,首项 ,且
,且 依次成等比数列,则该数列的通项公式
依次成等比数列,则该数列的通项公式 ,数列
,数列 的前6项和为 .
的前6项和为 .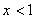 , 则
, 则 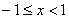 ”的逆否命题是“若
”的逆否命题是“若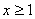 , 则
, 则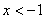 或
或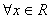 ,
, 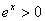 ”的否定是“
”的否定是“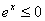 ”;
”;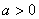 ”是“函数
”是“函数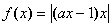 在区间
在区间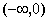 上单调递减”的充要条件;
上单调递减”的充要条件;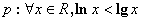 ;命题
;命题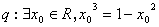 , 则 “
, 则 “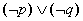 为真命题”.
为真命题”. 的共轭复数是 ( )
的共轭复数是 ( )