题目内容
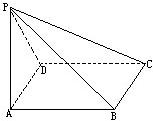 四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PC=
四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PC=| 2 |
分析:先根据AB,AP,PB的长判断PA⊥AB,同时AD⊥AB判断出AB⊥平面PAD,进而推断出面PAB⊥面PAD,面PAD⊥面ABCD;利用CD∥AB推断出CD⊥平面PAD进而可知面PAD⊥面PCD.
解答:解:∵AB=AP=a,PB=
a
∴AB2+AP2=PB2,
∴PA⊥AB
∵AD⊥AB
∴AB⊥平面PAD,
∵AB?平面ABCD,AB?平面PAB
∴面PAB⊥面PAD,面PAD⊥面ABCD,
∵CD∥AB
∴CD⊥平面PAD
∵CD?面PDC
∴面PAD⊥面PCD
故答案为面PAB⊥面PAD,面PAD⊥面ABCD,面PAD⊥面PCD
| 2 |
∴AB2+AP2=PB2,
∴PA⊥AB
∵AD⊥AB
∴AB⊥平面PAD,
∵AB?平面ABCD,AB?平面PAB
∴面PAB⊥面PAD,面PAD⊥面ABCD,
∵CD∥AB
∴CD⊥平面PAD
∵CD?面PDC
∴面PAD⊥面PCD
故答案为面PAB⊥面PAD,面PAD⊥面ABCD,面PAD⊥面PCD
点评:本题主要考查了平面与平面的垂直的判定.考查了学生对立体几何基础知识的掌握.

练习册系列答案
相关题目
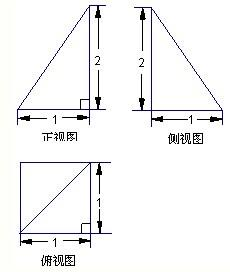 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
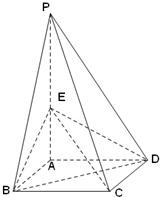 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: