题目内容
已知函数 ,x∈R.
,x∈R.
(Ⅰ)若a=3,求曲线y=f(x)在点x=2处的切线方程;
(Ⅱ)若对任意的x∈[-1,2],都有f(x)>0恒成立,求a的取值范围.
解:(Ⅰ)a=3时,f(x)=x3-x2+2,f(2)=6,f'(x)=3x2-2x,f'(2)=8,
∴切线方程为:y=8x-10
(Ⅱ)f'(x)=x(ax-2),
(1)a=0时,f'(x)=-2x,f(2)=-2<0,不符合题意,所以a≠0;
(2)f'(x)=x(ax-2)=0,x=0或 ,
,
当 ,即a≥1时,
,即a≥1时,
由a≥1得, .
.
∴只需 且
且 ,解得1≤a<3
,解得1≤a<3
(3) ,即0<a<1时,
,即0<a<1时,
0<a<1时, ,只需
,只需 ,解得
,解得
(4)a<0时, ,不符合题意.
,不符合题意.
综上, .
.
分析:(Ⅰ)确定切点的坐标,求导函数,确定切线的斜率,即可得到切线方程;
(Ⅱ)求导函数,再分类讨论:(1)a=0时,不符合题意;(2)a≠0时,f'(x)=x(ax-2)=0,x=0或 ,确定函数的最值,结合f(x)>0恒成立,即可求a的取值范围.
,确定函数的最值,结合f(x)>0恒成立,即可求a的取值范围.
点评:本题考查导数知识的运用,考查导数的几何意义,考查分类讨论的数学思想,考查恒成立问题,正确求导,合理分类是关键.
∴切线方程为:y=8x-10
(Ⅱ)f'(x)=x(ax-2),
(1)a=0时,f'(x)=-2x,f(2)=-2<0,不符合题意,所以a≠0;
(2)f'(x)=x(ax-2)=0,x=0或
 ,
,当
 ,即a≥1时,
,即a≥1时,| x | -1 | (-1,0) | 0 | 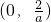 |  |  | 2 |
| f'(x) | + | 0 |  | 0 | + | ||
| f(x) | 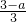 | 增 | 极大值2 | 减 | 极小值 | 增 |  |
 .
.∴只需
 且
且 ,解得1≤a<3
,解得1≤a<3(3)
 ,即0<a<1时,
,即0<a<1时,| x | -1 | (-1,0) | 0 | (0,2) | 2 |
| f'(x) | + | 0 |  | ||
| f(x) | 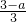 | 增 | 极大值2 | 减 |  |
 ,只需
,只需 ,解得
,解得
(4)a<0时,
 ,不符合题意.
,不符合题意.综上,
 .
.分析:(Ⅰ)确定切点的坐标,求导函数,确定切线的斜率,即可得到切线方程;
(Ⅱ)求导函数,再分类讨论:(1)a=0时,不符合题意;(2)a≠0时,f'(x)=x(ax-2)=0,x=0或
 ,确定函数的最值,结合f(x)>0恒成立,即可求a的取值范围.
,确定函数的最值,结合f(x)>0恒成立,即可求a的取值范围.点评:本题考查导数知识的运用,考查导数的几何意义,考查分类讨论的数学思想,考查恒成立问题,正确求导,合理分类是关键.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.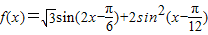 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.