题目内容
【题目】若存在直线l与曲线![]() 和曲线
和曲线![]() 都相切,则称曲线
都相切,则称曲线![]() 和曲线
和曲线![]() 为“相关曲线”,有下列四个命
为“相关曲线”,有下列四个命
题:
①有且只有两条直线l使得曲线![]() 和曲线
和曲线![]() 为“相关曲线”;
为“相关曲线”;
②曲线![]() 和曲线
和曲线![]() 是“相关曲线”;
是“相关曲线”;
③当![]() 时,曲线
时,曲线![]() 和曲线
和曲线![]() 一定不是“相关曲线”;
一定不是“相关曲线”;
④必存在正数![]() 使得曲线
使得曲线![]()
![]() 和曲线
和曲线![]()
![]() 为“相关曲线”.
为“相关曲线”.
其中正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
①判断两圆相交即可;②判断两双曲线是共轭双曲线即可;③判断两曲线可能相切即可;;④假设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 都相切,切点分别为
都相切,切点分别为![]() ,根据公切线重合,判断方程
,根据公切线重合,判断方程![]() 有实数解即可.
有实数解即可.
①圆心![]() ,半径
,半径![]() ,圆心
,圆心![]() ,半径
,半径![]() ,
,![]() ,因为
,因为![]() ,所以曲线
,所以曲线![]() 与曲线
与曲线![]() 有两条公切线,所以①正确;②曲线
有两条公切线,所以①正确;②曲线![]() 和曲线
和曲线![]() 是“相关曲线”是共轭双曲线(一部分),没有公切线,②错误;③由
是“相关曲线”是共轭双曲线(一部分),没有公切线,②错误;③由![]() ,消去
,消去![]() ,得:
,得:![]() ,即
,即![]() ,令
,令![]() 得:
得:![]() ,当
,当![]() 时,曲线
时,曲线![]() 与曲线
与曲线![]() 相切,所以存在直线
相切,所以存在直线![]() 与曲线
与曲线![]() 与曲线
与曲线![]() 都相切,所以③错误;④假设直线
都相切,所以③错误;④假设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 都相切,切点分别为
都相切,切点分别为![]() 和
和![]() ,
,![]() ,
,![]() ,所以分别以
,所以分别以![]() 和
和![]() 为切点的切线方程为
为切点的切线方程为![]() ,
,![]() ,由
,由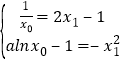 得:
得:![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,得:
,得:![]() (舍去)或
(舍去)或![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,所以方程
,所以方程![]() 有实数解,所以存在直线
有实数解,所以存在直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 都相切,所以④正确.所以正确命题的个数是
都相切,所以④正确.所以正确命题的个数是![]() ,故选B.
,故选B.

练习册系列答案
相关题目