题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .函数
.函数![]() 的导函数
的导函数![]() 在
在![]() 上存在零点.
上存在零点.
![]() 求实数
求实数![]() 的取值范围;
的取值范围;
![]() 若存在实数
若存在实数![]() ,当
,当![]() 时,函数
时,函数![]() 在
在![]() 时取得最大值,求正实数
时取得最大值,求正实数![]() 的最大值;
的最大值;
![]() 若直线
若直线![]() 与曲线
与曲线![]() 和
和![]() 都相切,且
都相切,且![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】![]()
![]() ;
;![]() 4;
4;![]() 12.
12.
【解析】
![]() 由题意可知,
由题意可知,![]() ,求导函数
,求导函数![]() ,方程
,方程![]() 在区间
在区间![]() 上有实数解,求出实数
上有实数解,求出实数![]() 的取值范围;
的取值范围;
![]() 由
由![]() ,则
,则![]() ,分步讨论,并利用导函数在函数的单调性的研究,得出正实数
,分步讨论,并利用导函数在函数的单调性的研究,得出正实数![]() 的最大值;
的最大值;
![]() 设直线
设直线![]() 与曲线
与曲线![]() 的切点为
的切点为![]() ,因为
,因为![]() ,所以切线斜率
,所以切线斜率![]() ,切线方程为
,切线方程为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 的切点为
的切点为![]() ,因为
,因为![]() ,所以切线斜率
,所以切线斜率![]() ,即切线方程为
,即切线方程为![]() ,
,
整理得![]() .所以
.所以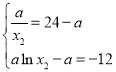 ,求得
,求得![]() ,设
,设![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,最后求出实数
上单调递增,最后求出实数![]() 的值.
的值.
![]() 由题意可知,
由题意可知,![]() ,则
,则![]() ,
,
即方程![]() 在区间
在区间![]() 上有实数解,解得
上有实数解,解得![]() ;
;
![]() 因为
因为![]() ,则
,则![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,不符题意;
上单调递增,不符题意;
②当![]() 时,令
时,令![]() ,
,
解得:![]() ,
,
当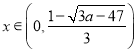 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以不存在![]() ,使得
,使得![]() 在
在![]() 上的最大值为
上的最大值为![]() ,不符题意;
,不符题意;
③当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]()
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
若![]() ,则
,则![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
若![]() ,则
,则![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
由题意可知,![]() ,即
,即![]() ,
,
整理得![]() ,
,
因为存在![]() ,符合上式,所以
,符合上式,所以![]() ,解得
,解得![]() ,
,
综上,![]() 的最大值为4;
的最大值为4;
![]() 设直线
设直线![]() 与曲线
与曲线![]() 的切点为
的切点为![]() ,
,
因为![]() ,所以切线斜率
,所以切线斜率![]() ,
,
即切线方程![]()
整理得:![]()
由题意可知,![]() ,即
,即![]() ,
,
即![]() ,解得
,解得![]()
所以切线方程为![]() ,
,
设直线![]() 与曲线
与曲线![]() 的切点为
的切点为![]() ,
,
因为![]() ,所以切线斜率
,所以切线斜率![]() ,即切线方程为
,即切线方程为![]() ,
,
整理得![]() .
.
所以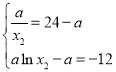 ,消去
,消去![]() ,整理得
,整理得![]() ,
,
且因为![]() ,解得
,解得![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() .
.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某种新型嫁接巨丰葡萄,在新疆地区种植一般亩产不低于5千斤,产量高的达到上万斤.受嫁接年限的影响,其产量一般逐年衰减,若在新疆地区平均亩产量低于5千斤,则从新嫁接.以下是新疆某地区从2014年开始嫁接后每年的平均亩产量y(单位:千斤)的数据表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
平均亩产量y | 8.2 | 7.8 | 7.2 | 6.6 | 5.4 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归直线方程,预计哪一年开始从新嫁接.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: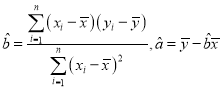 .
.