题目内容
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
| x |  |  |  |  |  |  | 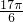 |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(Ⅱ)求当
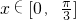 时,y=f(3x)的值域.
时,y=f(3x)的值域.
解:(I)依题意,函数最大值为3且相邻两个最大值点的差为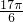 -
- =2π
=2π
∴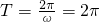 ,得ω=1
,得ω=1
又∵
∴ ,结合
,结合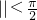 ,得
,得
∴函数y=f(x)的解析式是 ;
;
(II)∵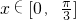 ,
,
∴ ,得
,得 的最小值为-
的最小值为- ,最大值为1
,最大值为1
∴y=f(3x)的值域为
分析:(I)根据相邻两个最大值点的距离得到函数的周期,再用周期公式得到ω=1,利用一组相邻的最大、最小值联列方程组解出A、B的值,再根据一个特殊的对应值列式解出φ值,从而得到函数y=f(x)的解析式;
(II)根据x的范围得到3x的范围,从而有 的最小值为-
的最小值为- ,最大值为1,得到y=f(3x)的值域.
,最大值为1,得到y=f(3x)的值域.
点评:本题根据三角函数y=Asin(ωx+φ)上的部分图象,得到函数解析式,并求y=f(3x)当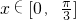 时的值域.着重考查了三角函数图象变换、解析式的求法和复合三角函数的值域等知识,属于基础题.
时的值域.着重考查了三角函数图象变换、解析式的求法和复合三角函数的值域等知识,属于基础题.
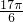 -
- =2π
=2π∴
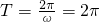 ,得ω=1
,得ω=1又∵

∴
 ,结合
,结合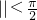 ,得
,得
∴函数y=f(x)的解析式是
 ;
;(II)∵
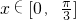 ,
,∴
 ,得
,得 的最小值为-
的最小值为- ,最大值为1
,最大值为1∴y=f(3x)的值域为

分析:(I)根据相邻两个最大值点的距离得到函数的周期,再用周期公式得到ω=1,利用一组相邻的最大、最小值联列方程组解出A、B的值,再根据一个特殊的对应值列式解出φ值,从而得到函数y=f(x)的解析式;
(II)根据x的范围得到3x的范围,从而有
 的最小值为-
的最小值为- ,最大值为1,得到y=f(3x)的值域.
,最大值为1,得到y=f(3x)的值域.点评:本题根据三角函数y=Asin(ωx+φ)上的部分图象,得到函数解析式,并求y=f(3x)当
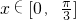 时的值域.着重考查了三角函数图象变换、解析式的求法和复合三角函数的值域等知识,属于基础题.
时的值域.着重考查了三角函数图象变换、解析式的求法和复合三角函数的值域等知识,属于基础题. 
练习册系列答案
相关题目
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
(1)根据表格提供的数据求函数y=f(x)的解析式;
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0), 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
 的一系列对应值如下表:
的一系列对应值如下表:| x |  |  |  |  |  |  |  |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0),
 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.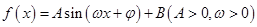 的一系列对应值如下表:
的一系列对应值如下表:







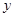



 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.  的一系列对应值如下表:
的一系列对应值如下表:






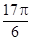



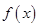 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.