题目内容
已知函数
的一系列对应值如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）根据表格提供的数据求函数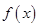
的一个解析式；
（2）根据（1）的结果，若函数
周期为
，当
时，方程
恰有两个不同的解，求实数
的取值范围.
【答案】
解：（1）设
的最小正周期为
，得
，
由
， 得
，
又
，解得
令
，即
，解得
，
∴
.
（2）∵函数
的周期为
，
又
， ∴
，
令
，∵
， ∴
，
如图，
在
上有两个不同的解，则
，
∴方程
在
时恰好有两个不同的解，则
，
即实数
的取值范围是
.
【解析】略
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
的一系列对应值如下表：
的解析式；
时，求方程
的解.
的一系列对应值如下表：
的一个解析式；
周期为
，当
时，方程
恰有两个不同的解，求实数
的取值范围；
已知函数
的一系列对应值如下表：
（1）根据表格提供的数据求函数y=f（x）的解析式；
（2）（文）当x∈[0，2π]时，求方程f（x）=2B的解．
（3）（理）若对任意的实数a，函数y=f（kx）（k＞0），
的图象与直线y=1有且仅有两个不同的交点，又当
时，方程f（kx）=m恰有两个不同的解，求实数m的取值范围．
的一系列对应值如下表：| x |  |  |  |  |  |  |  |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
（2）（文）当x∈[0，2π]时，求方程f（x）=2B的解．
（3）（理）若对任意的实数a，函数y=f（kx）（k＞0），
的图象与直线y=1有且仅有两个不同的交点，又当时，方程f（kx）=m恰有两个不同的解，求实数m的取值范围．
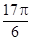
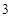
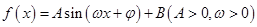的一系列对应值如下表：
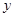
的一个解析式；
周期为
，当
时，方程
恰有两个不同的解，求实数
的取值范围.