题目内容
(本题12分)设 是公比大于1的等比数列,已知
是公比大于1的等比数列,已知 ,且
,且 构成等差数列.
构成等差数列.
(1)求数列 的通项公式.(2)令
的通项公式.(2)令 求数列
求数列 的前
的前 项和
项和 .
.
【答案】
(1) 的通项为
的通项为 .(2)
.(2)
【解析】本试题主要是考查了等差数列、等比数列的通项公式,以及数列的求和的综合运用。
(1)由已知得 解得
解得 .设数列
.设数列 的公比为
的公比为 ,由
,由 ,可得
,可得 ,解得
,解得 ,然后得到结论
,然后得到结论
(2)由于
由(1)得

那么 是等差数列,利用公式求和。
是等差数列,利用公式求和。
解:(1)由已知得 解得
解得 .
.
设数列 的公比为
的公比为 ,由
,由 ,可得
,可得 .
.
又 ,可知
,可知 ,即
,即 ,解得
,解得 .
.
由题意得 .
. .故数列
.故数列 的通项为
的通项为 .
.
(2)由于
由(1)得

又
 是等差数列.
是等差数列.

 故
故

练习册系列答案
相关题目
 是公差
是公差 的等差数列,
的等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, .
. …),求数列
…),求数列 的前
的前 项和
项和 .
.
 的表达式;
的表达式; 的单调区间、极大值、极小值。
的单调区间、极大值、极小值。 是定义在
是定义在 上的增函数,令
上的增函数,令
 时定值;
时定值; 在
在 ,求证
,求证 。
。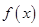 是定义在
是定义在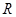 上的增函数,令
上的增函数,令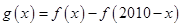
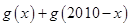 时定值;
时定值;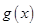 在
在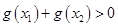 ,求证
,求证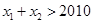 。
。