题目内容
已知集合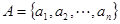 ,其中
,其中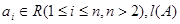 表示和
表示和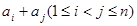 中所有不同值的个数.
中所有不同值的个数.
(Ⅰ)若集合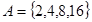 ,则
,则 ;
;
(Ⅱ)当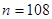 时,
时,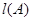 的最小值为____________.
的最小值为____________.
(Ⅰ)6;(Ⅱ)213.
解析试题分析:(Ⅰ)因为2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,故有6个不同值.所以 ;(Ⅱ)当
;(Ⅱ)当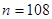 时,将集合
时,将集合 中元素按从小到大顺序重新排列,得
中元素按从小到大顺序重新排列,得 ,且
,且 .依题意,和
.依题意,和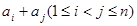 可以组成
可以组成 、
、 、
、 …、
…、 、
、 、…、
、…、 、
、 、…
、… 、……、
、……、 共5778个.且易知
共5778个.且易知 <
< <
< <…<
<…< ;
; <
< <…<
<…< ;……
;…… .当只要
.当只要 ,就有
,就有 时,和
时,和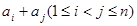 中所有不同值的个数最少,因为
中所有不同值的个数最少,因为 为这些值中的最小值,
为这些值中的最小值, 为这些值中的最大值.所以
为这些值中的最大值.所以 .故
.故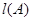 的最小值为213.
的最小值为213.
考点:新概念的理解

练习册系列答案
相关题目
设集合 ,
, ,若
,若 ,则
,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
 ,
, ,且
,且 ,则实数
,则实数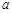 的值是 .
的值是 . ,
, ,如果
,如果
 ,则
,则 .
. 中的元素
中的元素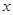 应满足的条件是 .
应满足的条件是 .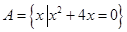
 .
. 求a的值;
求a的值; ,求a的值;
,求a的值; ,也可表示为{a2,a+b,0},则a2 013+b2 013=________.
,也可表示为{a2,a+b,0},则a2 013+b2 013=________.