题目内容
【题目】近年来，我国大力发展新能源汽车工业，新能源汽车(含电动汽车)销量已跃居全球首位．某电动汽车厂新开发了一款电动汽车．并对该电动汽车的电池使用情况进行了测试，其中剩余电量y与行驶时问
(单位：小时)的测试数据如下表：
（1）根据电池放电的特点，剩余电量y与行驶时间之间满足经验关系式：
，通过散点图可以发现y与之间具有相关性．设
，利用表格中的前8组数据求相关系数r，并判断是否有99％的把握认为与
之间具有线性相关关系；(当相关系数r满足
时，则认为有99％的把握认为两个变量具有线性相关关系)
（2）利用与的相关性及表格中前8组数据求出
与之间的回归方程；(结果保留两位小数)
（3）如果剩余电量不足0.8，电池就需要充电．从表格中的10组数据中随机选出8组，设X表示需要充电的数据组数，求X的分布列及数学期望．
附：相关数据：
．
表格中前8组数据的一些相关量：
，
，
相关公式：对于样本
，其回归直线
的斜率和戗距的最小二乘估计公式分别为：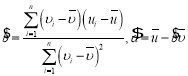
，
相关系数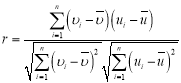
．
【答案】（1）
；有99%的把握认为
与
之间具有线性相关关系（2）
（3）见解析，3.2
【解析】
（1）先求出相关系数，即得有99%的把握认为
之间具有线性相关关系；
（2）先求出
，再求出所求的回归方程为
；
（3）由题得X的所有可能取值为2，3，4，再求出对应的概率，即得X的分布列及数学期望．.
解：（1）由题意知，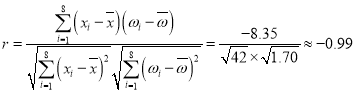
.
因为
，所以有99%的把握认为之间具有线性相关关系.
（2）对
两边取对数得
，
设
，
，
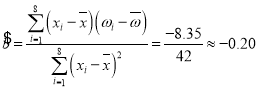易知
.
所以.
所以所求的回归方程为.
（3）10组数据中需要充电的数据组数为4组，X的所有可能取值为2，3，4.
.
所以X的分布列如下：
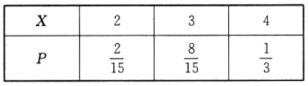
所以X的数学期望为
.
练习册系列答案
相关题目
