题目内容
定义在R上的偶函数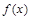 满足
满足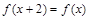 且
且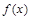 在
在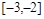 上是减函数,又
上是减函数,又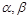 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )
A.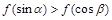 | B.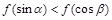 |
C.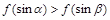 | D.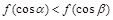 |
A
解析试题分析:由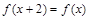 得函数周期为2,在
得函数周期为2,在 上为减函数,所以在
上为减函数,所以在 上为减函数,函数是定义在R上的偶函数,根据对称性得
上为减函数,函数是定义在R上的偶函数,根据对称性得 上为增函数,
上为增函数, 是锐角三角形的两个内角,有
是锐角三角形的两个内角,有 ,那么
,那么 ,由余弦函数性质与诱导公式,得
,由余弦函数性质与诱导公式,得 ,所以
,所以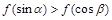 .
.
考点:1.函数的奇偶性、周期性、单调性;2.余弦函数的性质与诱导公式.

练习册系列答案
相关题目
设定义域为R的函数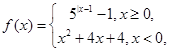 若关于x的方程
若关于x的方程 有7个不同的实数解,则m=( ).
有7个不同的实数解,则m=( ).
| A.2 | B.4或6 | C.2或6 | D.6 |
(5分)(2011•陕西)方程|x|=cosx在(﹣∞,+∞)内( )
| A.没有根 | B.有且仅有一个根 | C.有且仅有两个根 | D.有无穷多个根 |
已知函数 ,则下列说法错误的是( )
,则下列说法错误的是( )
A.若 ,则 ,则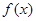 有零点 有零点 |
B.若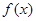 有零点,则 有零点,则 且 且 |
C. 使得 使得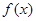 有唯一零点 有唯一零点 |
D.若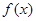 有唯一零点,则 有唯一零点,则 且 且 |
已知函数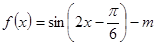 在
在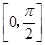 上有两个零点,则
上有两个零点,则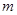 的取值范围是( )
的取值范围是( )
A.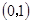 | B.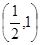 | C.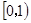 | D.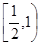 |
已知函数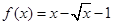 ,
,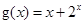 ,
, 的零点分别为
的零点分别为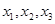 ,则( )
,则( )
A.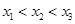 | B.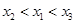 | C.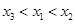 | D.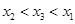 |
若f(x)为奇函数,且在(-∞,0)内是增函数,又f(-2)=0,则xf(x)<0的解集为( )
| A.(-2,0)∪(0,2) | B.(-∞,-2)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-2,0)∪(2,+∞) |
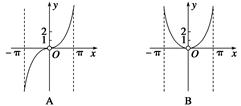
 ,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )