题目内容
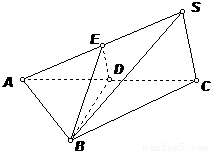
如图,已知三棱锥S-ABC中,底面△ABC是边长为2的正三角形,SC=1,∠SCA=90°,侧面SAC与底面ABC所成二面角为60°,E、D分别为SA和AC的中点.
(1)求点S到平面BDE的距离;
(2)求三棱锥S-ABC的体积.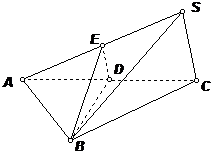
(1)求点S到平面BDE的距离;
(2)求三棱锥S-ABC的体积.


(1)∵E、D分别为SA和AC的中点,
∴ED∥SC
∵∠SCA=90°,
∴ED∥AC,
∴点S到平面BDE的距离等于点C到平面BDE的距离,设为h,
∵底面△ABC是边长为2的正三角形
∴BD⊥AC
∵侧面SAC与底面ABC所成二面角为60°
∴∠BDE=60°
∵底面△ABC是边长为2的正三角形,SC=1,
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 8 |
∵E到平面DBC的距离为
| ||
| 4 |
| ||
| 2 |
∴由等体积可得
| 1 |
| 3 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 3 |
| 3 |
| 8 |
∴h=1;
(2)∵E到平面DBC的距离为
| ||
| 4 |
| ||
| 2 |
∵S△ABC=
| 3 |
∴三棱锥S-ABC的体积为
| 1 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
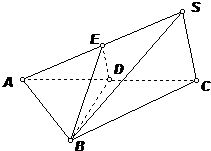 如图,已知三棱锥S-ABC中,底面△ABC是边长为2的正三角形,SC=1,∠SCA=90°,侧面SAC与底面ABC所成二面角为60°,E、D分别为SA和AC的中点.
如图,已知三棱锥S-ABC中,底面△ABC是边长为2的正三角形,SC=1,∠SCA=90°,侧面SAC与底面ABC所成二面角为60°,E、D分别为SA和AC的中点.
 AB,N为AB
AB,N为AB 上一点,
上一点,