题目内容
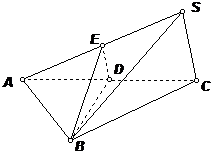
如图,已知三棱锥S-ABC中,底面△ABC是边长为2的正三角形,SC=1,∠SCA=90°,侧面SAC与底面ABC所成二面角为60°,E、D分别为SA和AC的中点.(1)求点S到平面BDE的距离;
(2)求三棱锥S-ABC的体积.
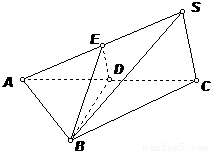
【答案】分析:(1)确定点S到平面BDE的距离等于点C到平面BDE的距离,利用等面积,即可求解;
(2)利用三棱锥的体积公式,即可求出结论.
解答: 解:(1)∵E、D分别为SA和AC的中点,
解:(1)∵E、D分别为SA和AC的中点,
∴ED∥SC
∵∠SCA=90°,
∴ED∥AC,
∴点S到平面BDE的距离等于点C到平面BDE的距离,设为h,
∵底面△ABC是边长为2的正三角形
∴BD⊥AC
∵侧面SAC与底面ABC所成二面角为60°
∴∠BDE=60°
∵底面△ABC是边长为2的正三角形,SC=1,
∴ =
=
∵E到平面DBC的距离为 ,S△BDC=
,S△BDC=
∴由等体积可得
∴h=1;
(2)∵E到平面DBC的距离为 ,∴S到平面DBC的距离为
,∴S到平面DBC的距离为 ,
,
∵
∴三棱锥S-ABC的体积为 =
= .
.
点评:本题考查点面距离的计算,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.
(2)利用三棱锥的体积公式,即可求出结论.
解答:
 解:(1)∵E、D分别为SA和AC的中点,
解:(1)∵E、D分别为SA和AC的中点,∴ED∥SC
∵∠SCA=90°,
∴ED∥AC,
∴点S到平面BDE的距离等于点C到平面BDE的距离,设为h,
∵底面△ABC是边长为2的正三角形
∴BD⊥AC
∵侧面SAC与底面ABC所成二面角为60°
∴∠BDE=60°
∵底面△ABC是边长为2的正三角形,SC=1,
∴
 =
=
∵E到平面DBC的距离为
 ,S△BDC=
,S△BDC=
∴由等体积可得

∴h=1;
(2)∵E到平面DBC的距离为
 ,∴S到平面DBC的距离为
,∴S到平面DBC的距离为 ,
,∵

∴三棱锥S-ABC的体积为
 =
= .
.点评:本题考查点面距离的计算,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
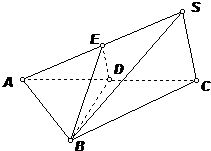 如图,已知三棱锥S-ABC中,底面△ABC是边长为2的正三角形,SC=1,∠SCA=90°,侧面SAC与底面ABC所成二面角为60°,E、D分别为SA和AC的中点.
如图,已知三棱锥S-ABC中,底面△ABC是边长为2的正三角形,SC=1,∠SCA=90°,侧面SAC与底面ABC所成二面角为60°,E、D分别为SA和AC的中点.
 AB,N为AB
AB,N为AB 上一点,
上一点,