题目内容
11．某校为了解1000名高一新生的身体生长状况，用系统抽样法（按等距的规则）抽取40名同学进行检查，将学生从1～1000进行编号，现已知第18组抽取的号码为443，则第一组用简单随机抽样抽取的号码为18．分析 根据系统抽样的特征，从1000名学生从中抽取一个容量为40的样本，抽样的分段间隔为$\frac{1000}{40}$=25，结合从第18组抽取的号码为443，可得第一组用简单随机抽样抽取的号码．
解答 解：∵从1000名学生从中抽取一个容量为40的样本，
∴系统抽样的分段间隔为$\frac{1000}{40}$=25，
设第一部分随机抽取一个号码为x，
则抽取的第18编号为x+17×25=443，∴x=18．
故答案为18．
点评 本题考查了系统抽样方法，关键是求得系统抽样的分段间隔．
练习册系列答案
相关题目
19．若将函数f（x）=sin（2x+$\frac{π}{6}$）的图象向左平移$\frac{π}{4}$个单位长度，再向下平移1个单位长度，得到函数g（x）的图象，则g（x）的一个对称中心为（ ）
| A． | （$\frac{π}{6}$，-1） | B． | （$\frac{π}{3}$，-1） | C． | （$\frac{π}{6}$，0） | D． | （$\frac{π}{3}$，0） |
2．设函数g（x）是R上的偶函数，当x＜0时，g（x）=ln（1-x），函数$f（x）=\left\{\begin{array}{l}{x^3}，x≤0\\ g（x），x＞0\end{array}\right.$满足f（2-x2）＞f（x），则实数x的取值范围是（ ）
| A． | （-∞，1）∪（2，+∞） | B． | （-∞，-2）∪（1，+∞） | C． | （1，2） | D． | （-2，1） |
19．已知向量$\overrightarrow a\;，\;\;\overrightarrow b$都是非零向量，“$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}|•|{\overrightarrow b}|$”是“$\overrightarrow a∥\overrightarrow b$”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充分必要条件 | D． | 既非充分也非必要条件 |
6．下列四个函数中是R上的减函数的为（ ）
| A． | $y={log_2}{2^{-x}}$ | B． | $y={（{\frac{1}{2}}）^{-x}}$ | C． | $y=\frac{1}{x+1}$ | D． | y=x2 |
进位制是人们为了计数和运算方便而约定的记数系统，在日常生活中，我们最熟悉、最常用的是十进制．如图是实现将某进制数a化为十进制数b的程序框图，若输入的k=2，a=110，n=3，则输出的b=（ ）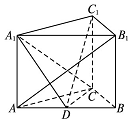
如图，在直三棱柱ABC-A1B1C1中，AB=4，AC=BC=3D为AB的中点，AB1⊥A1C