Question

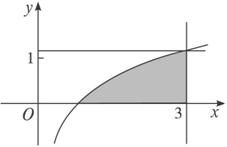
利用随机模拟法计算图中阴影部分（曲线y=2^x与x轴，x=±1围成的部分）的面积.

Answer 1

分析：在坐标系中画出正方形，用随机模拟的方法可以求出阴影部分与正方形面积之比，从而求得阴影部分面积的近似值.

解：（1）利用计算机产生两组［0，1］上的均匀随机数，a₁=rand，b₁=rand；

（2）进行平移和伸缩变换，a=(a₁-0.5)*2，b=b₁*2，得到一组［-1，1］上的均匀随机数和一组［0，2］上的均匀随机数；

（3）统计试验总次数N和落在阴影内的点数N₁（满足条件b＜2^a的点(a,b)个数）；

（4）计算频率，即为点落在阴影部分的概率的近似值；

（5）用几何概率公式求得点落在阴影部分的概率为P=，即.

∴S=，即为阴影部分的面积的近似值.

绿色通道

    解决本题的关键是利用随机模拟法和几何概型概率公式分别求得几何概率，然后通过解方程求得阴影部分面积的近似值.随机模拟计算的步骤：

（1）构造图形（作图）.

（2）模拟投点，计算落在阴影部分的点的频率mn.

（3）利用mn≈P(A)=算出相应的量.