题目内容
平面直角坐标系中,直线 的参数方程是
的参数方程是 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求直线 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线 与曲线
与曲线 相交于
相交于 两点,求
两点,求 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)先消去参数 求得直线的普通方程,然后将极坐标与直角坐标的关系式
求得直线的普通方程,然后将极坐标与直角坐标的关系式 代入直线方程,根据特殊角的三角函数值即可求解;(Ⅱ)直线的极坐标方程与曲线的极坐标方程联立方程组,消去一个未知数,求得
代入直线方程,根据特殊角的三角函数值即可求解;(Ⅱ)直线的极坐标方程与曲线的极坐标方程联立方程组,消去一个未知数,求得 ,根据方程的根与系数的关系以及两点间的距离公式求解.
,根据方程的根与系数的关系以及两点间的距离公式求解.
试题解析:(Ⅰ)消去参数得直线 的直角坐标方程为:
的直角坐标方程为: . 2分
. 2分
由 代入得,
代入得, ,
,
解得 .
.
(也可以是: 或
或 .) 5分
.) 5分
(Ⅱ)由 得,
得, ,
,
设 ,
, ,则
,则 . 10分
. 10分
考点:1.参数方程与普通方程的互化;2.两点间的距离公式;3.极坐标方程的简单应用;4.特殊角的三角函数值

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 .
. 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 ,求|MA|·|MB|.
,求|MA|·|MB|. ,半径R=
,半径R= ,求圆C的极坐标方程.
,求圆C的极坐标方程. (
( ,
, 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1, )对应的参数j=
)对应的参数j= ,曲线C2过点D(1,
,曲线C2过点D(1, )在曲线C1上,求
)在曲线C1上,求 的值.
的值. 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 的直角坐标方程;
的直角坐标方程; 中,曲线
中,曲线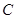 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线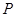 的方程为
的方程为 .
. 、
、 ,求
,求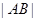 .
. 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点,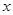 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线 的方程为
的方程为 .
. 、
、 ,求
,求 .
.
 (t为参数),直线l与曲线C相交于A、B两点求|AB|的值
(t为参数),直线l与曲线C相交于A、B两点求|AB|的值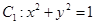 ,将
,将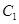 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的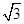 、2倍后得到曲线
、2倍后得到曲线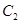 . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线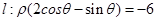 .
.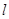 的直角坐标方程和曲线
的直角坐标方程和曲线