题目内容
在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)求直线 的直角坐标方程;
的直角坐标方程;
(2)求点 到曲线
到曲线 上的点的距离的最小值.
上的点的距离的最小值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)将点 极坐标
极坐标 ,化为直角坐标,然后在直线坐标系中求直线
,化为直角坐标,然后在直线坐标系中求直线 的方程;(2)由曲线
的方程;(2)由曲线 的参数方程化为普通方程为
的参数方程化为普通方程为 ,再数形结合考虑点
,再数形结合考虑点 到曲线
到曲线 上的点的距离的最小值.
上的点的距离的最小值.
试题解析:(1)∵点 的极坐标为
的极坐标为 ,∴
,∴ ,点
,点 的直角坐标为
的直角坐标为
(4,4),∴直线 的直角坐标方程
的直角坐标方程 ;
;
(2) 由曲线C的参数方程 (
( 为参数),化成普通方程为:
为参数),化成普通方程为: ,表示以
,表示以 为圆心,半径为
为圆心,半径为 的圆,由于点
的圆,由于点 在曲线C外,故点M到曲线C上的点的距离最小值为
在曲线C外,故点M到曲线C上的点的距离最小值为 .
.
考点:1、极坐标和直角坐标的转化;2、参数方程和普通方程的互化.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 中,圆的参数方程为
中,圆的参数方程为 ,以坐标原点
,以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.求:
轴的正半轴为极轴建立极坐标系.求: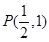 ,倾斜角α=
,倾斜角α=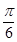 ,圆C的极坐标方程为
,圆C的极坐标方程为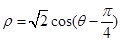 .
. 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 的普通方程与曲线
的普通方程与曲线 得到曲线
得到曲线 ,设
,设 为曲线
为曲线 的最小值,并求相应点
的最小值,并求相应点 的坐标.
的坐标.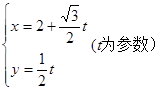 的直线
的直线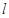 ,被以原点为极点,
,被以原点为极点, 轴的正半轴为极轴,极坐标方程为
轴的正半轴为极轴,极坐标方程为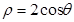 的曲线
的曲线 所截,求截得的弦长.
所截,求截得的弦长. 的参数方程是
的参数方程是 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
. 两点,求
两点,求 .
. 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线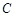 的极坐标方程为
的极坐标方程为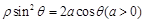 ,过点
,过点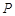 (-2,-4)的直线
(-2,-4)的直线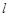 的参数方程为
的参数方程为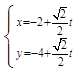 (
(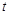 为参数),直线
为参数),直线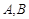 两点.
两点. ,求
,求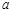 的值.
的值.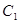 的方程为
的方程为 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线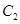 的参数方程为
的参数方程为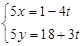 (
(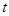 为参数).
为参数).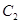 的普通方程;
的普通方程; 为曲线
为曲线 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围. 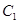 的参数方程为
的参数方程为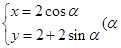 为参数),M为
为参数),M为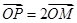 ,点P的轨迹为曲线
,点P的轨迹为曲线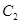 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线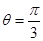 与
与