Question

20．已知正实数m，n满足2＜m+2n＜4，则m²+n²的取值范围是$（\frac{4}{5}，16）$．

Answer 1

分析 正实数m，n满足2＜m+2n＜4，如图所示，分别作出直线m=-2n+2，m=-2n+4．设圆O：m²+n²=r²．（r＞0）当⊙O与直线m=-2n+2相切时，利用点到直线的距离公式求出r；⊙O经过点Q（0，4），求出r．即可得出．

解答 解：正实数m，n满足2＜m+2n＜4，如图所示，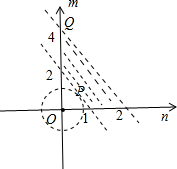
分别作出直线m=-2n+2，m=-2n+4．
设圆O：m²+n²=r²．（r＞0）
当⊙O与直线m=-2n+2相切时，$r=\frac{2}{\sqrt{5}}$，r²=$\frac{4}{5}$．
⊙O经过点Q（0，4），r²=16．
∴$\frac{4}{5}$＜m²+n²＜16．
∴m²+n²的取值范围是$（\frac{4}{5}，16）$．
故答案为：$（\frac{4}{5}，16）$．

点评 本题考查了直线与圆相切、线性规划有关知识，考查了数形结合方法、推理能力与计算能力，属于中档题．