Question

【题目】已知函数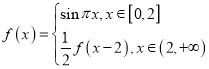，有下列说法：

①函数对任意，都有成立；

②函数在上单调递减；

③函数在上有3个零点；

④若函数的值域为，设是中所有有理数的集合，若简分数（其中，为互质的整数），定义函数，则在中根的个数为5；

其中正确的序号是______（填写所有正确结论的番号）.

Answer 1

【答案】②③④

【解析】

画出函数图像，结合图像，以及函数性质，对选项进行逐一分析.

根据函数解析式，画出函数的图像如下图所示：

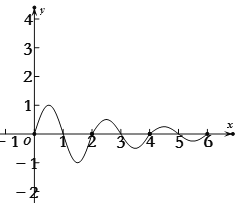
对①，因为，故成立，

则不成立，故①不正确；

对②，在内，函数在单调递减，根据图像可知，

函数的单调区间为，故②正确；

对③，在同一直角坐标系中画出与的图像：

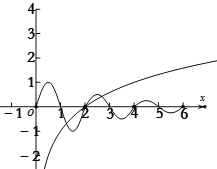
由图可知，两函数有3个交点，故有三个零点，

故③正确；

对④，由图可知，，故，

根据题意可得，解得，

又因为，且均为整数，

故是小于24，且是3的倍数，同时还满足的自然数，

故由此得的取值如下：

，，；,，

合计5种可能.故在中根的个数为5.故④正确.

故答案为：②③④.