题目内容
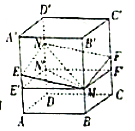
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
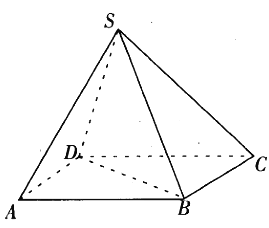
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析;(2)![]()
【解析】试题分析:(Ⅰ)首先利用正弦定理求得![]() ,由此可推出
,由此可推出![]() ,然后利用勾股定理推出
,然后利用勾股定理推出![]() ,从而使问题得证;(Ⅱ)利用等积法将问题转化为
,从而使问题得证;(Ⅱ)利用等积法将问题转化为![]() 求解即可.
求解即可.
试题解析:(Ⅰ)证明:在![]() 中,
中, ![]() ,由已知
,由已知![]() ,
, ![]() ,
, ![]() ,
,
解得![]() ,所以
,所以![]() ,即
,即![]() ,可求得
,可求得![]() .
.
在![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)由题意可知, ![]() 平面
平面![]() ,则
,则![]() 到面
到面![]() 的距离等于
的距离等于![]() 到面
到面![]() 的距离,
的距离,
在![]() 中,易求
中,易求![]() ,
,
![]() ,
,
且![]() ,
, ![]() 面
面![]() ,
,
则![]() ,即
,即![]() ,则
,则![]() ,
,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

点睛:垂直、平行关系证明中应用转化与化归思想的常见类型,(1)证明线面、面面平行,需转化为证明线线平行;(2)证明线面垂直,需转化为证明线线垂直;(3)证明线线垂直,需转化为证明线面垂直.

练习册系列答案
相关题目
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
根据表中信息解答以下问题:
(1)从该单位任选两名职工,求这两人休年假次数之和为4的概率;
(2)从该单位任选两名职工,用![]() 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.