题目内容
如果过抛物线y=x2+x上的点P做切线平行于直线y=2x的切线，那么这切线方程是______．
设切点P（x0，y0），∵y′=2x+1，又切线平行于直线y=2x，
∴2x0+1=2，解得x0=
．
∴y0=(
)2+
=
．
∴切线方程为y-
=2(x-
)，化为8x-4y-1=0．
故答案为8x-4y-1=0．
∴2x0+1=2，解得x0=
| 1 |
| 2 |
∴y0=(
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∴切线方程为y-
| 3 |
| 4 |
| 1 |
| 2 |
故答案为8x-4y-1=0．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
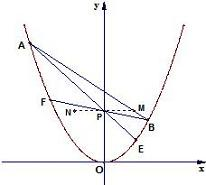已知抛物线y=x2和三个点M（x0，y0）、P（0，y0）、N（-x0，y0）（y0≠x02，y0＞0），过点M的一条直线交抛物线于A、B两点，AP、BP的延长线分别交曲线C于E、F．