题目内容
设有关于x的一元二次方程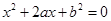 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
⑴ ;⑵
;⑵ .
.
解析试题分析:⑴先列举出满足条件“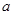 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数”的所有的基本事件,再在基本事件中找到满足条件“
三个数中任取的一个数”的所有的基本事件,再在基本事件中找到满足条件“ ”的基本事件
”的基本事件 的个数,用基本事件
的个数,用基本事件 的个数除以总的事件的个数,所得的比值即是所求;⑵根据
的个数除以总的事件的个数,所得的比值即是所求;⑵根据 的取值画出满足条件“
的取值画出满足条件“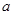 是从区间
是从区间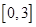 任取的一个数,
任取的一个数, 是从区间
是从区间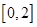 任取的一个数”的长方形区域,以及在此条件下满足“
任取的一个数”的长方形区域,以及在此条件下满足“ ”的基本事件的三角形区域,所求的概率即是两个图形的面积比.
”的基本事件的三角形区域,所求的概率即是两个图形的面积比.
试题解析:设事件 为“方程
为“方程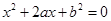 有实根”.
有实根”.
当 时,方程
时,方程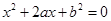 有实根的充要条件为
有实根的充要条件为 .
.
基本事件共有 个:
个: .
.
其中第一个数表示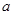 的取值,第二个数表示
的取值,第二个数表示 的取值.
的取值.
事件 中包含9个基本事件, 4分
中包含9个基本事件, 4分
事件 发生的概率为
发生的概率为 . 6分
. 6分
如图所示:
试验的全部结果所构成的区域为 ,对应长方形
,对应长方形 , 8分
, 8分
构成事件 的区域为
的区域为 ,对应图中的阴影部分, 10分
,对应图中的阴影部分, 10分
所以所求的概率为 . 12分
. 12分
考点:1.离散型随机变量及其应用;2.连续性随机变量及其应用;3.古典概型;4.几何概型

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案为了解某市市民对政府出台楼市限购令的态度,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令的赞成人数如下表:
| 月收入 |  | [25,35) | [35,45) |  |  |  |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 8 | 5 | 2 | 1 |
(Ⅰ)根据已知条件完成下面的2×2列联表,有多大的把握认为赞不赞成楼市限购令与收入高低有关?
已知:
 ,
,当
 <2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
<2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;当
 >2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;
>2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;当
 >3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;
>3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;当
 >6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。
>6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。| | 非高收入族 | 高收入族 | 总计 |
| 赞成 | | | |
| 不赞成 | | | |
| 总计 | | | |
某品牌汽车的4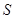 店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4
店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4 店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用
店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用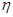 表示经销一辆该品牌汽车的利润.
表示经销一辆该品牌汽车的利润.
| 付款方式 | 一次 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
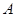 :“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率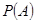 ;
;(2)求
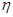 的分布列及其数学期望
的分布列及其数学期望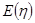 .
.  表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求
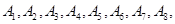 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为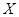 .若
.若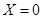 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.
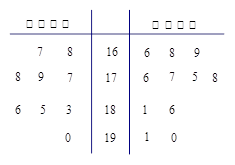
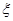 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出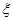 ,求随机变量
,求随机变量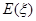 .
.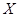 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求