题目内容
函数
，则f（x）的导函数f′（x）的奇偶性是
- A.奇函数
- B.偶函数
- C.既是奇函数又是偶函数
- D.非奇非偶函数
D
分析：先由函数求得导函数，再利用奇偶性的定义来判断，先看定义域是否关于原点对称，再看f（-x）与f（x）的关系．
解答：∵
∴f′（x）=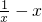
由f（x）知其定义域为：[0，+∞）
不关于原点对称，
所以是非奇非偶函数，
故选D
点评：本题主要考查判断函数的奇偶性，先看定义域是否关于原点对称，再看f（-x）与f（x）的关系，同时还要注意原函数与导函数中的自变量一致．
分析：先由函数求得导函数，再利用奇偶性的定义来判断，先看定义域是否关于原点对称，再看f（-x）与f（x）的关系．
解答：∵
∴f′（x）=
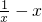
由f（x）知其定义域为：[0，+∞）
不关于原点对称，
所以是非奇非偶函数，
故选D
点评：本题主要考查判断函数的奇偶性，先看定义域是否关于原点对称，再看f（-x）与f（x）的关系，同时还要注意原函数与导函数中的自变量一致．
练习册系列答案
相关题目
，则f（x）的导函数f′（x）的奇偶性是（ ）