题目内容
设
、
不共线,
=2
-
,
=3
-2
,试判断
、
能否作为基底.
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由共线的向量不能作为平面向量的一组基底,分析向量
、
是否共线,能求出结果.
| c |
| d |
解答:
解:若非零向量
、
共线,
则存在非零实数λ,使
=λ
,
即2
-
=λ(3
-2
),
即(2-3λ)
=(1-2λ)
,
∵
、
不共线,2-3λ和1-2λ不能同时为零,
故(2-3λ)
=(1-2λ)
不可能成立,
故假设不成立,
即向量
、
不共线,
故向量
不共线是两不共线的向量,
∴断
、
能作为基底.
| c |
| d |
则存在非零实数λ,使
| c |
| d |
即2
| a |
| b |
| a |
| b |
即(2-3λ)
| a |
| b |
∵
| a |
| b |
故(2-3λ)
| a |
| b |
故假设不成立,
即向量
| c |
| d |
故向量
不共线是两不共线的向量,
∴断
| c |
| d |
点评:本题考查平行向量的性质和应用,是基础题.解题时要认真审题,正确解题的关键是知道共线的向量不能作为平面向量的一组基底.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
礼堂第一排有a个座位,后面每一排比前一排多一个座位,则第n排的座位是( )
| A、n+1 |
| B、a+(n+1) |
| C、a+n |
| D、a+(n-1) |
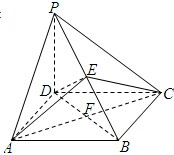 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6