Question

13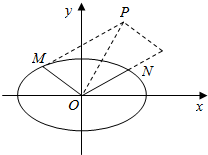．如图所示，已知M，N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点，且直线OM与ON的斜率之积为-$\frac{1}{2}$（其中O为坐标原点），若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$．问：是否存在两个定点F₁，F₂，使得|PF₁|+|PF₂|为定值．若存在，求F₁，F₂的坐标；若不存在，说明理由．

Answer 1

分析 设出P，M，N的坐标，根据题设等式建立等式，把M，N代入椭圆方程，整理求得x²+2y²20+4（x₁x₂+2y₁y₂），设出直线OM，ON的斜率，利用题意可求得x₁x₂+2y₁y₂=0，进而求得x²+2y²的值，利用椭圆的定义可推断出|PF₁|+|PF₂|为定值求得c，则两定点坐标可得．

解答 解：设P（x，y），M（x₁，y₁），N（x₂，y₂），
则由$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$，得（x，y）=（x₁，y₁）+2（x₂，y₂），
即x=x₁+2x₂，y=y₁+2y₂，
∵点M，N在椭圆上，所以$\frac{{{x}_{1}}^{2}}{4}$+$\frac{{{y}_{1}}^{2}}{2}$=1，$\frac{{{x}_{2}}^{2}}{4}$+$\frac{{{y}_{2}}^{2}}{2}$=1，
故x²+2y²=（x₁²+4x₂²+4x₁x₂）+2（y₁²+4y₂²+4y₁y₂）=20+4（x₁x₂+2y₁y₂），
设k_0M，k_ON分别为直线OM，ON的斜率，根据题意可知k_0Mk_ON=-$\frac{1}{2}$，
∴x₁x₂+2y₁y₂=0，
∴x²+2y²=20，
所以P在椭圆$\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{10}$=1上；
设该椭圆的左，右焦点为F₁，F₂，
由椭圆的定义可推断出|PF₁|+|PF₂|为定值，因为c=$\sqrt{10}$，
则这两个定点坐标是（-$\sqrt{10}$，0）（$\sqrt{10}$，0）．

点评 本题主要考查了椭圆的简单性质．同时考查向量加法的平行四边形法则，考查了学生分析问题和解决问题的能力．