题目内容
3．已知函数y=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x，求函数的振幅、角速度、初相位．分析 把函数化为y=Asin（ωx+φ）的形式，即可得出函数的振幅、角速度与初相位．
解答 解：∵函数y=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x
=cos$\frac{π}{3}$sin2x+sin$\frac{π}{3}$cos2x
=sin（2x+$\frac{π}{3}$），
∴函数y的振幅为A=1，
角速度为ω=2，
初相位为φ=$\frac{π}{3}$．
点评 本题考查了三角函数y=Asin（ωx+φ）的图象与性质的应用问题，是基础题目．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
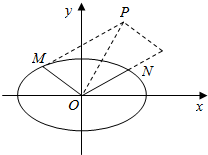如图所示，已知M，N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点，且直线OM与ON的斜率之积为-$\frac{1}{2}$（其中O为坐标原点），若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$．问：是否存在两个定点F1，F2，使得|PF1|+|PF2|为定值．若存在，求F1，F2的坐标；若不存在，说明理由．
14．如果a，b，c∈R，那么“b2＞4ac”是“方程ax2+bx+c=0有两个不等实根”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
11．已知角α的终边经过点P（-1，3），则2sinα+cosα=（ ）
| A． | $\frac{\sqrt{10}}{2}$ | B． | $\frac{\sqrt{10}}{10}$ | C． | $-\frac{7\sqrt{10}}{10}$ | D． | $-\frac{\sqrt{10}}{2}$ |
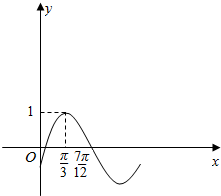函数f（x）=sin（ωx+φ）（ω＞0．|φ|＜$\frac{π}{2}$）的图象部分如图所示．