题目内容
3.已知关于x,y的不等式$\frac{|x|}{a}+\frac{|y|}{3}≤1$(a>0)所表示的平面区域的面积为24,则a的值为4.分析 根据题意,得出不等式$\frac{|x|}{a}+\frac{|y|}{3}≤1$(a>0)所表示的平面区域是以点(±a,0),(0,±3)为顶点的菱形,根据菱形的面积求出a的值.
解答 解:根据对称性,知;
不等式$\frac{|x|}{a}+\frac{|y|}{3}≤1$(a>0)所表示的平面区域是:
四个点(±a,0),(0,±3)为顶点的菱形,
则该菱形的面积为$\frac{1}{2}$•2a•2•3=24,
解得a=4.
故答案为:4.
点评 本题考查了不等式组表示的平面区域的应用问题,是基础题目.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
18.已知点A,B,C,D为同一球面上的四点,且AB=AC=AD=2,AB⊥AC,AC⊥AD,AD⊥AB,则这个球的表面积是( )
| A. | 16π | B. | 20π | C. | 12π | D. | 8π |
8.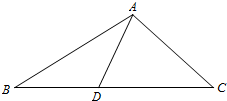 如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
 如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{3}}{6}$ |
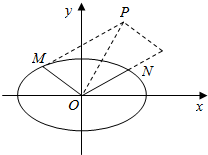 如图所示,已知M,N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点,且直线OM与ON的斜率之积为-$\frac{1}{2}$(其中O为坐标原点),若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$.问:是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值.若存在,求F1,F2的坐标;若不存在,说明理由.
如图所示,已知M,N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点,且直线OM与ON的斜率之积为-$\frac{1}{2}$(其中O为坐标原点),若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$.问:是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值.若存在,求F1,F2的坐标;若不存在,说明理由.