题目内容
1．已知{$\frac{1}{{a}_{n}}$}是等差数列，且a1=1，a4=4，则a10=（ ）| A． | -$\frac{4}{5}$ | B． | -$\frac{5}{4}$ | C． | $\frac{4}{13}$ | D． | $\frac{13}{4}$ |
分析 根据题意，设等差数列{$\frac{1}{{a}_{n}}$}的公差为d，结合题意可得$\frac{1}{{a}_{1}}$=1，$\frac{1}{{a}_{4}}$=$\frac{1}{4}$，计算可得公差d的值，进而由等差数列的通项公式可得$\frac{1}{{a}_{10}}$的值，求其倒数可得a10的值．
解答 解：根据题意，{$\frac{1}{{a}_{n}}$}是等差数列，设其公差为d，
若a1=1，a4=4，有$\frac{1}{{a}_{1}}$=1，$\frac{1}{{a}_{4}}$=$\frac{1}{4}$，
则3d=$\frac{1}{{a}_{4}}$-$\frac{1}{{a}_{1}}$=-$\frac{3}{4}$，即d=-$\frac{1}{4}$，
则$\frac{1}{{a}_{10}}$=$\frac{1}{{a}_{1}}$+9d=-$\frac{5}{4}$，
故a10=-$\frac{4}{5}$；
故选：A．
点评 本题考查等差数列的通项公式，注意求出{$\frac{1}{{a}_{n}}$}的公差．
练习册系列答案
相关题目
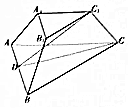已知三棱台ABC-A1B1C1中，AB=BC=4，AC=2A1C1=2$\sqrt{2}$，AA1=CC1=1，平面AA1B1B⊥平面AA1C1C．
12．若x＞2m2-3是-1＜x＜4的必要不充分条件，则实数m的取值范围是（ ）
| A． | [-3，3] | B． | （-∞，-3]∪[3，+∞） | C． | （-∞，-1]∪[1，+∞） | D． | [-1，1] |
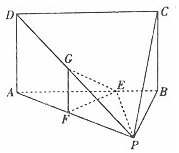在四棱锥P-ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，AB=AP=3，AD=PB=2，E为线段AB上一点，且AE：EB=7：2，点F、G分别为线段PA、PD的中点．
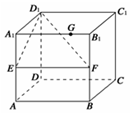在棱长为1的正方体ABCD-A1B1C1D1中，E、F分别为棱AA1、BB1的中点，G为棱A1B1上的一点，且A1G=λ（0≤λ≤1），则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$．