��Ŀ����
��ͼ������ƽ��ֱ������ϵxOy��x���ڵ�ƽ���ϣ�y�ᴹֱ�ڵ�ƽ�棬��λ����Ϊ1ǧ�ף�ij��λ������ԭ�㣮��֪�ڵ������Ĺ켣�ڷ���y��kx�� (1��k2)x2 (k>0)��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮
(1��k2)x2 (k>0)��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮

(1)���ڵ������̣�
(2)���ڵ�һ������һ������(�������С)������и߶�Ϊ3.2ǧ�ף��������ĺ�����a����������ʱ���ڵ����Ի���������˵�����ɣ�
�⡡(1)��y��0����kx�� (1��k2)x2��0��
(1��k2)x2��0��
��ʵ���������������֪x>0����k>0��
�� ��
��
���ҽ���k��1ʱȡ�Ⱥţ�
�����ڵ�������Ϊ10ǧ�ף�
(2)��Ϊa>0�������ڵ��ɻ���Ŀ��⇔����k>0��
ʹ3.2��ka�� (1��k2)a2����
(1��k2)a2����
⇔����k�ķ���a2k2��20ak��a2��64��0������
⇔�б�ʽ����(��20a)2��4a2(a2��64)��0⇔0<a��6.
���Ե�a������6ǧ��ʱ���ɻ���Ŀ�꣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
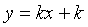 ����Բ
����Բ ��λ�ù�ϵ��( )
��λ�ù�ϵ��( )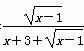 �����ֵΪ________��
�����ֵΪ________��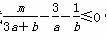 ���������m�����ֵΪ________��
���������m�����ֵΪ________��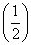 |1��x|��m��ͼ����x���й����㣬��ʵ��m��ȡֵ��Χ��________��
|1��x|��m��ͼ����x���й����㣬��ʵ��m��ȡֵ��Χ��________��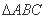 �У���
�У���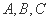 �ĶԱ߷ֱ�Ϊ
�ĶԱ߷ֱ�Ϊ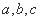 ����
����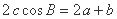 ����
���� ����
���� ����СֵΪ .
����СֵΪ . B.
B.  C.
C.  D.
D. 
