题目内容
11.△ABC的内角A、B、C的对边分别为a,b,c,ab=60,面积S△ABC=15$\sqrt{3}$,△ABC外接圆半径为$\sqrt{3}$,则c=3.分析 由题意和三角形的面积公式可得sinC,再由正弦定理可得c值.
解答 解:∵△ABC中ab=60,面积S△ABC=15$\sqrt{3}$,
∴S=$\frac{1}{2}$absinC=$\frac{1}{2}$×60×sinC=15$\sqrt{3}$,
解得sinC=$\frac{\sqrt{3}}{2}$,
∵△ABC外接圆半径R=$\sqrt{3}$,
∴由正弦定理可得c=2RsinC=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3.
故答案为:3.
点评 本题考查正弦定理解三角形,涉及三角形的面积公式,属基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
19.椭圆y2+$\frac{{x}^{2}}{{m}^{2}}$=1(0<m<1)上存在点P使得PF1⊥PF2,则m的取值范围是( )
| A. | [$\frac{\sqrt{2}}{2}$,1) | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{1}{2}$,1) | D. | (0,$\frac{1}{2}$] |
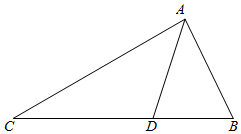 如图,在△ABC中,AC=16,∠C=$\frac{π}{6}$,点D在BC边上,且BD=6$\sqrt{3}$,tan∠ADB=$\frac{2\sqrt{3}}{3}$.
如图,在△ABC中,AC=16,∠C=$\frac{π}{6}$,点D在BC边上,且BD=6$\sqrt{3}$,tan∠ADB=$\frac{2\sqrt{3}}{3}$.