题目内容
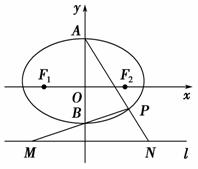
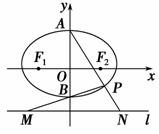
如图,椭圆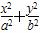 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直 线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为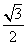 ,且过点A(0,1).
,且过点A(0,1).
(1)求k1·k2的值;
(2)求MN的最小值;
(3)随着点P的变化,以MN为直径的圆是否恒过定点?若过定点,求出该定点;如不过定点,请说明理由.
解 (1)因为e=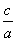 =
=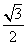 ,b=1,解得a=2,所以椭圆C的标准方程为
,b=1,解得a=2,所以椭圆C的标准方程为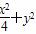 =1.(2分)
=1.(2分)
设椭圆上点P(x0,y0),有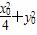 =1,
=1,
所以k1·k2=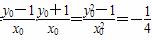 (2)因为M,N在直线l:y=-2上,设M(x1,-2),N(x2,-2),
(2)因为M,N在直线l:y=-2上,设M(x1,-2),N(x2,-2),
由方程知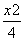 +y2=1知,A(0,1),B(0,-1),
+y2=1知,A(0,1),B(0,-1),
所以KBM·kAN=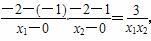 (6分)
(6分)
又由(1)知kAN·kBM=k1·k2=-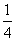 ,所以x1x2=-12,(8分)
,所以x1x2=-12,(8分)
不妨设x1<0,则x2>0,则
MN=|x1-x2|=x2-x1=x2+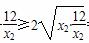 =4
=4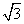 ,
,
所以当且仅当x2=-x1=2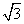 时,MN取得最小值4
时,MN取得最小值4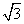 .(10分)
.(10分)
(3)设M(x1,-2),N(x2,-2),
则以MN为直径的圆的方程为
(x-x1)(x-x2)+(y+2)2=0,(12分)
即x2+(y+2)2-12-(x1+x2)x=0,若圆过定点,
则有x=0,x2+(y+2)2-12=0,解得x=0,y=-2±2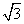 ,
,
所以,无论点P如何变化,以MN为直径的圆恒过定点(0,-2±2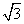 ).(16分)
).(16分)

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 ,从这
,从这 条线段中任取
条线段中任取 条,则所取
条,则所取 的零点分别为
的零点分别为 的大小关系是
的大小关系是 B.
B. 
 D.
D. 
 =1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
=1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
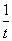 ,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.
,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|. x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+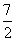 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数). ,点P、M、N分别为BC1、CC1、AB1
,点P、M、N分别为BC1、CC1、AB1