题目内容
 如图,A、B是海面上位于东西方向相距5(3+
如图,A、B是海面上位于东西方向相距5(3+| 3 |
| 3 |
考点:解三角形的实际应用
专题:解三角形
分析:利用正弦定理
=
,求出BD,在△DCB中,利用余弦定理求出CD,利用正弦定理求出∠DCB推出结果.
| DB |
| sin45° |
| AB |
| sinD |
解答:
解:AB=5(3+
),∠D=105°,sinD=sin(60°+45°)=
由
=
得BD=10
…(4分)
在△DCB中,BC=20
,∠DBC=60°
CD=
=30
∴救援船到达D的时间为
=1小时…(8分)
由
=
得sin∠DCB=
∠DCB=30°
∴救援船的航行方向是北偏东30°的方向.…(12分)
| 3 |
| ||||
| 4 |
由
| DB |
| sin45° |
| AB |
| sinD |
得BD=10
| 3 |
在△DCB中,BC=20
| 3 |
CD=
(20
|
∴救援船到达D的时间为
| 30 |
| 30 |
由
| BD |
| sinDCB |
| CD |
| sin60° |
| 1 |
| 2 |
∠DCB=30°
∴救援船的航行方向是北偏东30°的方向.…(12分)
点评:本题考查正弦定理以及余弦定理的应用,解三角形的时间问题的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
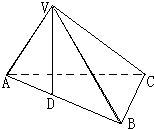 如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形.
如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形. 将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第1个数为
将全体正整数排成一个三角形数阵:按照以上排列的规律,第n行(n≥3)从左向右的第1个数为