题目内容
某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到 元.公司拟投入
元.公司拟投入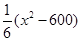 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
(1)40元;(2) 至少应达到10.2万件,每件定价为30元.
至少应达到10.2万件,每件定价为30元.
解析试题分析:(1)这是函数应用题中涉及销售的问题,要清楚知道常识性的等式:销售总收入=销售单价×销售量.提价为 元时,销售量是(
元时,销售量是( )万件,总收入为
)万件,总收入为 ,不低于原收入,得不等式
,不低于原收入,得不等式 ;(2)关键是弄懂原收入与总投入之和是多少?原收入
;(2)关键是弄懂原收入与总投入之和是多少?原收入 ,总投入
,总投入 ,明年的销售收入不低于原收入与总投入之和就是不等式
,明年的销售收入不低于原收入与总投入之和就是不等式

 ,根据问题的要求,此式变为
,根据问题的要求,此式变为 时,
时, 有解(注意不是恒成立),所以
有解(注意不是恒成立),所以 的范围是
的范围是 不小于
不小于 的最小值.
的最小值.
试题解析:(1)设每件定价为 元,依题意,有
元,依题意,有 ,
,
整理得 ,解得
,解得 .
.
∴要使销售的总收入不低于原收入,每件定价最多为40元. 7′
(2)依题意, 时,
时,
不等式 有解,等价于
有解,等价于 时,
时, 有解,
有解,  (当且仅当
(当且仅当 时,等号成立)
时,等号成立) .
.
∴当该商品明年的销售量 至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元. 14′
至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元. 14′
考点:函数的应用题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
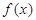 是
是 上的增函数,
上的增函数,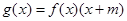 ,已知
,已知 .
.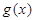 在
在 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;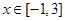 时,
时,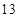 ,求实数
,求实数 R.
R.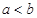 ,比较
,比较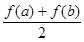 与
与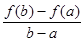 的大小并说明理由。
的大小并说明理由。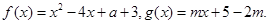
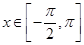 时,若函数
时,若函数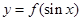 存在零点,求实数
存在零点,求实数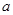 的取值范围并讨论零点个数;
的取值范围并讨论零点个数;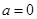 时,若对任意的
时,若对任意的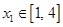 ,总存在
,总存在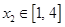 ,使
,使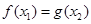 成立,求实数
成立,求实数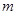 的取值范围.
的取值范围.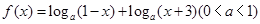
 的定义域;
的定义域; 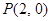 ,点
,点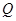 在曲线
在曲线 :
: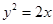 上.
上.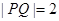 ,求点
,求点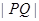 的最小值.
的最小值. (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度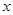 (单位:
(单位: )满足关系:
)满足关系:
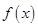 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。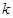 的值及
的值及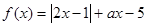 (a是常数,a∈R)
(a是常数,a∈R)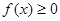 的解集;
的解集;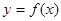 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.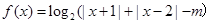 .
. 时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是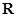 ,求
,求 的取值范围.
的取值范围.