题目内容
已知函数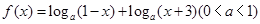
(1)求函数 的定义域;
的定义域;
(2)求函数 的零点;
的零点;
(3)若函数 的最小值为-4,求a的值.
的最小值为-4,求a的值.
(1)函数的定义域为 ;(2
;(2 的零点是
的零点是 ;(3)
;(3) .
.
解析试题分析:(1)函数的定义域是使函数有意义的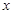 取值范围,而对数有意义则真数大于0,即
取值范围,而对数有意义则真数大于0,即 ;
;
(2)函数 的零点等价于方程
的零点等价于方程 的根,可先利用对数运算性质
的根,可先利用对数运算性质 进行化简,即
进行化简,即
 ,要注意定义域的范围,检验解得的根是否在定义域内;
,要注意定义域的范围,检验解得的根是否在定义域内;
(3)可利用函数的单调性求最值来解参数 ,由(2)可知
,由(2)可知 ,令
,令 ,
, 在
在 单调递减,则
单调递减,则 在
在 取最大值时函数
取最大值时函数 的最小值取-4,而
的最小值取-4,而 ,当
,当 时
时 ,则
,则
 ,
, .
.
试题解析:21.( 普通班)
(1)要使函数有意义,则有 解之得
解之得 ,
,
所以函数的定义域为 .
.
(2)函数可化为
由 ,得
,得 , 即
, 即 ,
, ,
, ,
, 的零点是
的零点是 .
.
21.(联办班)
(1)要使函数有意义:则有 ,解之得:
,解之得:  ,
,
所以函数的定义域为: .
.
(2)函数可化为
由 ,得
,得 ,即
,即 ,
, ,
, ,
, 的零点是
的零点是 .
.
(3)


 .
. ,
, ,
,  .由
.由 ,得
,得 ,
, .
.
考点:1、对数函数的定义域;2对数的运算性质;3、函数的零点;4、对数方程的解法;5、复合函数的最值问题;6、二次函数的最值.

练习册系列答案
相关题目
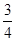 是省外游客,其余是省内游客.在省外游客中有
是省外游客,其余是省内游客.在省外游客中有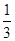 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
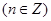 满足
满足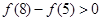 .
. 的解析式;
的解析式;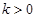 ,使
,使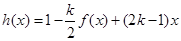 在区间
在区间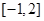 上的值域为
上的值域为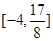 ?若存在,求出
?若存在,求出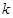 ;若不存在,请说明理由.
;若不存在,请说明理由. ,
,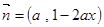 ,其中
,其中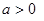 .函数
.函数 在区间
在区间 上有最大值为4,设
上有最大值为4,设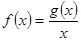 .
.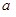 的值;
的值;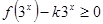 在
在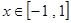 上恒成立,求实数
上恒成立,求实数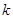 的取值范围.
的取值范围.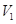 .
.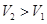 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。  元.公司拟投入
元.公司拟投入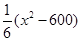 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. 吨,此时所需生产费用为(
吨,此时所需生产费用为(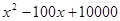 )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为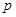 万元,这里
万元,这里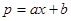 (
(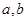 为常数,
为常数,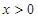 )
)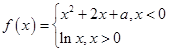 ,其中
,其中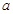 是实数,设
是实数,设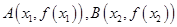 为该函数的图象上的两点,且
为该函数的图象上的两点,且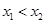 .
. 的单调区间;
的单调区间;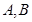 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求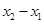 的最小值;
的最小值;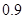 万元,年维修费用第一年是
万元,年维修费用第一年是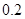 万元,第二年是
万元,第二年是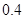 万元,第三年是
万元,第三年是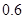 万元,…,以后逐年递增
万元,…,以后逐年递增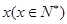 年的维修费用的和为
年的维修费用的和为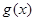 ,年平均费用为
,年平均费用为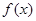 .
.