题目内容
如图(1),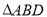 为等边三角形,
为等边三角形,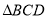 是以
是以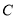 为直角顶点的等腰直角三角形且
为直角顶点的等腰直角三角形且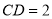 ,
,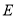 为线段
为线段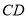 中点,将
中点,将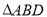 沿
沿 折起(如图2),使得线段
折起(如图2),使得线段 的长度等于
的长度等于 ,对于图二,完成以下各小题:
,对于图二,完成以下各小题:
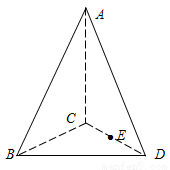
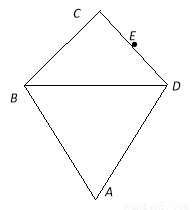
(图1) (图2)
(1)证明: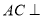 平面
平面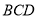 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)线段 上是否存在点
上是否存在点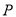 ,使得平面
,使得平面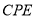 与平面
与平面 垂直?若存在,请求出线段
垂直?若存在,请求出线段 的长度;若不存在,请说明理由。
的长度;若不存在,请说明理由。
(1) 见解析
(2) 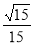
(3) 故线段AB上存在点P,此时线段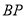 的长度为
的长度为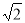
【解析】
试题分析:关于线面垂直的证明问题,注意把线面垂直的判定定理的内容记熟,对于线线、线面垂直的转化要熟悉,注意线面角的求法,并且第一步求出的直接结果就是线面角的正弦值,要看清要求的结果是谁,关于是否存在类问题,注意一般步骤,要先下结论,之后求解,能求出来就说明有,退出矛盾,就说明没有.
试题解析:(1)∵
又∵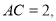 ∴
∴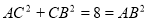 ∴
∴
同理可证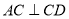 故
故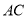 垂直面
垂直面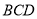 内两条相交直线
内两条相交直线
则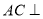 平面
平面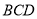 3分
3分
(2) 由(1)知 ,
,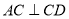 ,又有
,又有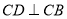
故可建如图所示建立空间直角坐标系C-xyz. 4分
∴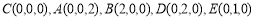
∴  ,
,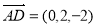 ,
,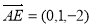 ,
,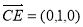
设平面ABD的一个法向量为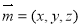 ,
,
则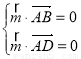
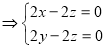 ,取
,取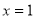 ,得
,得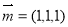 . 6分
. 6分
设直线AE与平面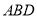 所成角为θ,
所成角为θ,
则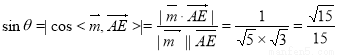 , 7分
, 7分
∴设直线AE与平面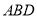 所成角的正弦值为
所成角的正弦值为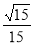 . 8分
. 8分
(3)假设存在符合条件的点P,并设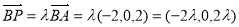 (
(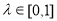 )
)
则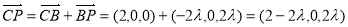
设平面CPE的一个法向量为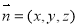 ,
,
则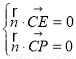
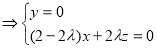 ,取
,取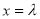 ,得
,得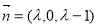 . 11分
. 11分
要使得平面CPE与平面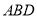 垂直,只需
垂直,只需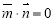 即
即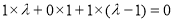
解得
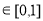 ,
,
故线段AB上存在点P,使得平面CPE与平面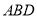 垂直,此时线段
垂直,此时线段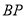 的长度为
的长度为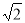 14分
14分
(说明:①答案提及“存在”而不能说明理由的得1分
②第(3)小题也可设P(2-t,0,t)展开解答)
考点:线面垂直,线面角,面面垂直.

 ,则目标函数
,则目标函数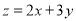 的最小值为( )
的最小值为( ) 、
、 满足条件
满足条件 则
则 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
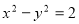 绕原点逆时针转动
绕原点逆时针转动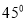 ,就会得到它的一条“任性双曲线”
,就会得到它的一条“任性双曲线”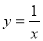 ;根据以上材料可推理得出双曲线
;根据以上材料可推理得出双曲线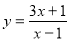 的焦距为( )
的焦距为( )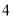 B.
B. 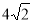 C.
C. 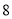 D.
D. 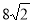
 ,且渐近线方程为
,且渐近线方程为 的双曲线方程是( )
的双曲线方程是( ) B.
B. C.
C. D.
D.
 :
: ;命题
;命题 :
: 。
。 为假命题,
为假命题, 为假命题,则求
为假命题,则求 的取值范围。
的取值范围。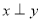 ,
,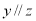 ,则
,则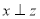 ”是假命题,那么字母
”是假命题,那么字母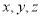 在空间所表示的几何图形可能是( )
在空间所表示的几何图形可能是( ) 全是直线 B.
全是直线 B.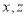 是直线,
是直线,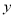 是平面 D.
是平面 D.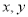 是平面,
是平面,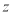 是直线
是直线 分别是与
分别是与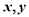 轴正方向同向的单位向量,平面内三点
轴正方向同向的单位向量,平面内三点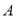 、
、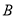 、
、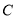 满足
满足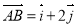 ,
, ,
,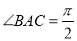 ,则实数m的值为 .
,则实数m的值为 . ,
, .
. 时,求
时,求 ;
; ,求实数
,求实数 的取值范围.
的取值范围.