题目内容
在边长为1的正△ABC中，设BC=a，CA=b，AB=c，则a﹒b+b﹒c+c﹒a=( )
A、
B、
C、
﹒
D、
【答案】
A
【解析】解：因为边长为1的正△ABC中，则BC=a，CA=b，AB=c，任意两个向量的所成的角都是1200，长度都为1，因此a+b+c=0，两边平方可得，3+2(a﹒b+b﹒c+c﹒a)=0
所以a﹒b+b﹒c+c﹒a=
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
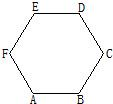
如图，在边长为1的正六边形ABCDEF中，下列向量的数量积中最大的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个水平放置的△ABC用斜二测画法画出的直观图是如图2-7-3所示的边长为1的正△A'B'C'，则在真实图形中AB边上的高是
（2012•泸州二模）如图，边长为1的正六边形ABCDEF中，向量