题目内容
(20)如图,在正四棱柱ABCD-A1B1C1D1中:AB=1,BB1=(Ⅰ)异面直线AD与C1G所成的角的大小;
(Ⅱ)二面角A-C1G-A1的正切值.


解法一:
(Ⅰ)由AD∥D
连接C![]() .再△FD
.再△FD![]() .
.
在Rt△C1D![]() 得∠C1GD1=
得∠C1GD1=![]() .
.
(Ⅱ)作D1H⊥C
在Rt△GHD1中,由D![]() ,∠D1GH=
,∠D1GH=![]() 得D1H=
得D1H=![]() .从而
.从而
tanD1HF=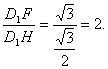
解法二:
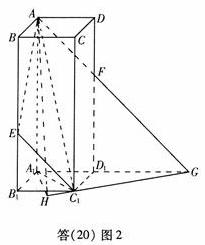
(Ⅰ)由AD∥D
因为EC1和AF是平行平面BB
由此可得∠AGA1=∠EC1B1=![]() ,
,
从而A![]() ,于是D
,于是D![]()
在Rt△C1D![]() 得∠C1GD1=
得∠C1GD1=![]()
(Ⅱ)在△A![]() ,∠A1GC1=
,∠A1GC1=![]() 知∠A
知∠A
在Rt△A1HG中,由A![]() ,∠A1GH=
,∠A1GH=![]() 得A1H=
得A1H=![]()
从而 tanAHA1=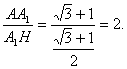
解法三:
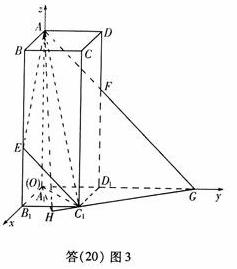
(Ⅰ)以A1为原点,A1B1,A1D1,A![]() +1),C1(1,1,0),D(0,1,
+1),C1(1,1,0),D(0,1,![]() +1),E(1,0,1)、
+1),E(1,0,1)、![]() =(0,1,0),
=(0,1,0),![]() =(0,1,-1)
=(0,1,-1)
因为EC1和AF分别是平行平面BB
则![]()
由![]() ∥
∥![]() 得
得![]() 于是y=
于是y=![]() +1.
+1.
故G(0,![]() +1,0)
+1,0)![]() (-1,
(-1,![]() ,0).
,0).
设异面直线AD与C
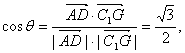
从而 θ=![]()
(Ⅱ)作A1H⊥C
设H(a,b,0),则![]()
由A1H⊥C![]() ,由此得a-
,由此得a-![]() b=0. ①
b=0. ①
又由H![]() ∥
∥![]() ,从而
,从而![]() 于是
于是
![]() ②
②
联立①和②得a=![]()
由|![]() 得
得
tan AHA1=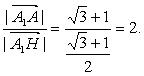

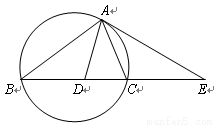
 现要设计一个如图所示的金属支架(图中实线所示),设计要求是:支架总高度AH为6米,底座BCDEF是以B为顶点,以CDEF为底面的正四棱锥,C,D,E,F在以半径为1米的圆上,支杆AB⊥底面CDEF.市场上,底座单价为每米10元,支杆AB单价为每米20元.设侧棱BC与底面所成的角为θ.
现要设计一个如图所示的金属支架(图中实线所示),设计要求是:支架总高度AH为6米,底座BCDEF是以B为顶点,以CDEF为底面的正四棱锥,C,D,E,F在以半径为1米的圆上,支杆AB⊥底面CDEF.市场上,底座单价为每米10元,支杆AB单价为每米20元.设侧棱BC与底面所成的角为θ. 如图,第n个图形是由正n+2边形“拓展”而来的.如图(1),在正三角形的每条边上,向外再“拓展”一个正三角形,得到一个有12个顶点的图形;如图(2),在正方形的四条边上向外“拓展”一个正方形,得到一个有20个顶点的图形,…,那么第n-2个图形中,共有
如图,第n个图形是由正n+2边形“拓展”而来的.如图(1),在正三角形的每条边上,向外再“拓展”一个正三角形,得到一个有12个顶点的图形;如图(2),在正方形的四条边上向外“拓展”一个正方形,得到一个有20个顶点的图形,…,那么第n-2个图形中,共有 中,
中,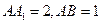 ,点
,点 是
是 的中点,点
的中点,点 在
在 上,设二面角
上,设二面角 的大小为
的大小为 。
。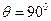 时,求
时,求 的长;
的长; 时,求
时,求 的长。
的长。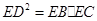 。
。
 中,设椭圆
中,设椭圆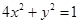 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。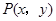 是椭圆
是椭圆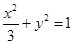 上的一个动点,求
上的一个动点,求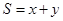 的最大值。
的最大值。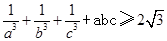 。
。