题目内容
1．如果不等式组$\left\{\begin{array}{l}{y≥0}\\{2x≥y}\\{kx-y+2≥0}\end{array}\right.$表示的平面区域是一个直角三角形，则该三角形的面积为（ ）| A． | $\frac{4}{5}$ | B． | $\frac{16}{5}$ | C． | $\frac{4}{5}$或$\frac{16}{5}$ | D． | $\frac{8}{5}$或$\frac{4}{5}$ |
分析 依题意，三条直线围成一个直角三角形，求出k的值，得到角点的坐标，利用三角形面积公式计算面积即可．
解答 解：作出平面区域，如图示：
若△OAB是RT△，
仅当l1⊥l2，得：k=-$\frac{1}{2}$，
A（4，0），B（$\frac{4}{5}$，$\frac{8}{5}$），△OAB的面积是$\frac{1}{2}$•4•$\frac{8}{5}$=$\frac{16}{5}$，
故选：B．
点评 本题主要考查了二元一次不等式表示平面区域的知识，直线的交点坐标的求法，直角三角形面积公式的运用，分类讨论的思想方法．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
9．已知函数f（x）=2sin（2x+φ）（|φ|＜$\frac{π}{2}$）在区间（-$\frac{π}{12}$，$\frac{π}{6}$]上单调且最大值不大于$\sqrt{3}$，则φ的取值范围是（ ）
| A． | [0，$\frac{π}{3}$] | B． | [$-\frac{π}{3}$，$\frac{π}{6}$] | C． | （$-\frac{π}{4}$，0] | D． | [$-\frac{π}{3}$，0] |
9．调查表明，市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性，现将这三项的满意度指标分别记为x、y、z，并对它们进行量化：0表示不满意，1表示基本满意，2表示满意，再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级：若ω≥4，则居住满意度为一级；若2≤?≤3，则居住满意度为二级；若0≤?≤1，则居住满意度为三级，为了解某城市居民对该城市的居住满意度，研究人员从此城市居民中随机抽取10人进行调查，得到如下结果：
（Ⅰ）若该城市有200万人常住人口，试估计该城市居民中居住满意度为三级的人数是多少？
（Ⅱ）从居住满意度为一级的被调查者中随机抽取两人，这两人的居住满意度指标ω均为4的概率是多少？
| 人员编号 | 1 | 2 | 3 | 4 | 5 |
| （x，y，z） | （1，1，2） | （2，1，1） | （2，2，2） | （0，1，1） | （1，2，1） |
| 人员编号 | 6 | 7 | 8 | 9 | 10 |
| （x，y，z） | （1，2，2） | （1，1，1） | （1，2，2） | （1，0，0） | （1，1，1） |
（Ⅱ）从居住满意度为一级的被调查者中随机抽取两人，这两人的居住满意度指标ω均为4的概率是多少？
16．执行如图所示程序框图，输出的a=（ ）
| A． | -1 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
6．关于x的方程asinx+bcosx+c=0在[0，π]上有两个相异实根α，β，则sin（α+β）=（ ）
| A． | $\frac{ab+bc+ac}{{a}^{2}+{b}^{2}+{c}^{2}}$ | B． | -$\frac{ab+bc+ac}{{a}^{2}+{b}^{2}+{c}^{2}}$ | ||
| C． | $\frac{2ab}{{a}^{2}+{b}^{2}}$ | D． | -$\frac{2ab}{{a}^{2}+{b}^{2}}$ |
13．
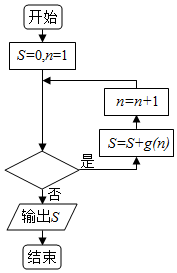已知函数f（x）=ax3+$\frac{1}{2}$x2在x=-1处取得极大值，记g（x）=$\frac{1}{f′（x）}$．在如图所示的程序框图中，若输出的结果S=$\frac{2016}{2017}$，则判断框中可以填入的关于n的判断条件是（ ）
已知函数f（x）=ax3+$\frac{1}{2}$x2在x=-1处取得极大值，记g（x）=$\frac{1}{f′（x）}$．在如图所示的程序框图中，若输出的结果S=$\frac{2016}{2017}$，则判断框中可以填入的关于n的判断条件是（ ）| A． | n≤2016？ | B． | n≤2017？ | C． | n＞2016？ | D． | n＞2017？ |