i为虚数单位.若复数z与(z+2)2-8i都是纯虚数.则z=( )A．2B．-2C．-2iD．2i 题目和参考答案——青夏教育精英家教网—

题目内容

12．i为虚数单位，若复数z与（z+2）²-8i都是纯虚数，则z=（　　）

A．

B．

-2

C．

-2i

D．

分析由题意设出z=ai（a≠0），代入（z+2）²-8i化简，再由（z+2）²-8i是纯虚数列式求得a值．

解答解：由题意可设z=ai（a≠0），
则（z+2）²-8i=（2+ai）²-8i=4-a²+（4a-8）i，
∵（z+2）²-8i是纯虚数，
∴$\left\{\begin{array}{l}{4-{a}^{2}=0}\\{4a-8≠0}\end{array}\right.$，解得a=-2．
∴z=-2i．
故选：C．

点评本题考查复数代数形式的混合运算，考查了复数的基本概念，是基础题．

练习册系列答案

3．在△ABC中，AB=1，AC=2，若G，H分别为△ABC的重心，外心，则$\overrightarrow{GH}•\overrightarrow{BC}$=$\frac{1}{2}$．

20．求过两圆x²+y²-4y-6=0，x²+y²-5x+y-6=0交点且过（2，1）的圆的方程．

7．求单调区间：f（x²）=$\frac{1}{{x}^{2}-2x-3}$．

17．

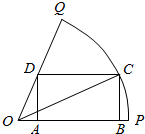如图，已知OPQ是半径为1，圆心角为$\frac{π}{3}$的扇形，C是扇形弧上的运动点，ABCD是扇形的内接矩形．记∠COP=α，求当角α取何值时，矩形ABCD的面积最大？并求出这个最大面积．
（1）找出S与α之间的函数关系；
（2）由得出的函数关系，求S的最大值．

4．已知函数f（x）=4cosxcos（x-$\frac{π}{3}$）-2．
（I）求函数f（x）的最小正周期；
（II）求函数f（x）在区间[-$\frac{π}{6}$，$\frac{π}{4}$]上的最大值和最小值．

1．已知函数在R上是单调函数，f（x）=$\left\{\begin{array}{l}{（3a-1）x+4a，x＜1}\\{lo{g}_{a}x，x≥1}\end{array}\right.$，则实数a的取值范围是$\frac{1}{7}$≤a＜$\frac{1}{3}$．

2．

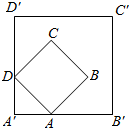如图所示，边长为1的正方形ABCD的顶点A，D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动，则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是（　　）

试题分类