题目内容
7．过定点（-2，0）的直线l与曲线C：（x-2）2+y2=4（0≤x≤3）交于不同的两点，则直线l的斜率的取值范围是$（{-\frac{{\sqrt{3}}}{3}，-\frac{{\sqrt{3}}}{5}}]∪[{\frac{{\sqrt{3}}}{5}，\frac{{\sqrt{3}}}{3}}）$．分析 画出图形，判断直线与曲线有两个交点的范围即可．
解答 解：过定点（-2，0）的直线l与曲线C：（x-2）2+y2=4（0≤x≤3）交于不同的两点，如图：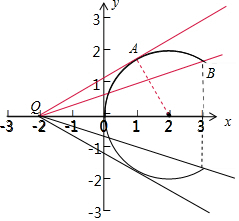
可得：k∈[kBQ，kAQ）．
B（3，$\sqrt{3}$），kBQ=$\frac{\sqrt{3}-0}{3+2}$=$\frac{\sqrt{3}}{5}$，
|AQ|=$\sqrt{16-4}$=2$\sqrt{3}$，kAQ=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
由对称性可知：直线的斜率的范围：$（{-\frac{{\sqrt{3}}}{3}，-\frac{{\sqrt{3}}}{5}}]∪[{\frac{{\sqrt{3}}}{5}，\frac{{\sqrt{3}}}{3}}）$．
故答案为：$（{-\frac{{\sqrt{3}}}{3}，-\frac{{\sqrt{3}}}{5}}]∪[{\frac{{\sqrt{3}}}{5}，\frac{{\sqrt{3}}}{3}}）$．
点评 本题考查直线与曲线交点问题，考查数形结合以及转化思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
18．
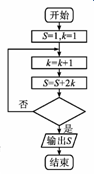某程序框图如图所示，若输出的S=29，则判断框内应填（ ）
某程序框图如图所示，若输出的S=29，则判断框内应填（ ）| A． | k＞5？ | B． | k＞4？ | C． | k＞7？ | D． | k＞6？ |
15．已知函数f（x）=$\frac{{lnx+{{（x-b）}^2}}}{x}$，若存在x∈[$\frac{1}{2}$，2]，使得xf'（x）+f（x）＞0，则实数b的取值范围是（ ）
| A． | $（-∞，\frac{3}{2}）$ | B． | $（-∞，\frac{3}{2}]$ | C． | $（-∞，\frac{9}{4}）$ | D． | $（-∞，\frac{9}{4}]$ |
12．
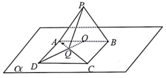如图，平面PAB⊥平面α，AB?α，且△PAB为正三角形，点D是平面α内的动点，ABCD是菱形，点O为AB中点，AC与OD交于点Q，I?α，且l⊥AB，则PQ与I所成角的正切值的最小值为（ ）
如图，平面PAB⊥平面α，AB?α，且△PAB为正三角形，点D是平面α内的动点，ABCD是菱形，点O为AB中点，AC与OD交于点Q，I?α，且l⊥AB，则PQ与I所成角的正切值的最小值为（ ）| A． | $\sqrt{-3+\frac{3\sqrt{7}}{2}}$ | B． | $\sqrt{3+\frac{3\sqrt{7}}{2}}$ | C． | $\sqrt{7}$ | D． | 3 |
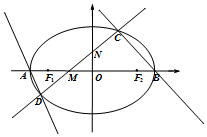如图，椭圆E的左右顶点分别为A、B，左右焦点分别为F1、F2，$|{AB}|=4，|{{F_1}{F_2}}|=2\sqrt{3}$，