题目内容
已知向量
=（2，-3），
=（x，6），且∥，则|+|的值为
- A.
- B.13
- C.
- D.5
C
分析：由向量共线的充要条件可得2×6-（-3）x=0，解得x=-4，故可得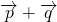
的坐标，由模长公式可得结果．
解答：由题意结合向量共线的充要条件可得：
2×6-（-3）x=0，解得x=-4
故+=（-2，3），
由模长公式可得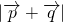
=
=
故选C
点评：本题为向量模长的求解，熟练利用公式是解决问题的关键，属基础题．
分析：由向量共线的充要条件可得2×6-（-3）x=0，解得x=-4，故可得
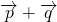的坐标，由模长公式可得结果．解答：由题意结合向量共线的充要条件可得：
2×6-（-3）x=0，解得x=-4
故
+=（-2，3），由模长公式可得
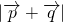==故选C
点评：本题为向量模长的求解，熟练利用公式是解决问题的关键，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知向量
=（-2，3），
=（x，6），则“x=9”是“
∥
”的（ ）
| a |
| b |
| a |
| b |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |