题目内容
已知 =(cosθ,2),
=(cosθ,2), =(
=( ,sinθ).
,sinθ).
(1)当 ∥
∥ ,且θ∈(
,且θ∈( ,
, )时,求cosθ-sinθ的值;
)时,求cosθ-sinθ的值;
(2)若 ⊥
⊥ ,求
,求 +
+ 的值.
的值.
解:(1)∵ ,∴
,∴ .
.
∴(sinθ-cosθ)2=1-2sinθcosθ= ,
,
∵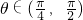 ,∴sinθ>cosθ,
,∴sinθ>cosθ,
∴ .
.
(2)∵ ,∴
,∴ .
.
∴cosθ=-10sinθ.
∴ +
+ =
= =
= =
=
= =
= =
= .
.
分析:(1)利用向量共线的充要条件及取锐角时的正弦值与余弦值的大小关系;
(2)利用 ?
? 即可得出sinθ与cosθ的大小关系,把原式通法化简利用平方关系即可得出.
即可得出sinθ与cosθ的大小关系,把原式通法化简利用平方关系即可得出.
点评:熟练掌握向量共线的充要条件、 ?
? 、三角函数的单调性、平方关系是解题的关键.
、三角函数的单调性、平方关系是解题的关键.
 ,∴
,∴ .
.∴(sinθ-cosθ)2=1-2sinθcosθ=
 ,
,∵
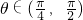 ,∴sinθ>cosθ,
,∴sinθ>cosθ,∴
 .
.(2)∵
 ,∴
,∴ .
.∴cosθ=-10sinθ.
∴
 +
+ =
= =
= =
=
=
 =
= =
= .
.分析:(1)利用向量共线的充要条件及取锐角时的正弦值与余弦值的大小关系;
(2)利用
 ?
? 即可得出sinθ与cosθ的大小关系,把原式通法化简利用平方关系即可得出.
即可得出sinθ与cosθ的大小关系,把原式通法化简利用平方关系即可得出.点评:熟练掌握向量共线的充要条件、
 ?
? 、三角函数的单调性、平方关系是解题的关键.
、三角函数的单调性、平方关系是解题的关键. 
练习册系列答案
相关题目
 ,则cos(π+2α)的值为( )
,则cos(π+2α)的值为( )



 ,则cos(π+2α)的值为( )
,则cos(π+2α)的值为( )


