题目内容
给定点P(2,-3),Q(3,2),已知直线ax+y+2=0与线段PQ(包括P,Q在内)有公共点,则a的取值范围是 .
【答案】分析:设出线段PQ上任一点M的坐标和一个定比,根据定比分点的公式,由P和Q的坐标表示出M的横纵坐标,将表示出的M坐标代入直线ax+y+2=0中,用含a的式子表示出t,由t的范围得到关于a的不等式,求出不等式的解集即可得到a的取值范围.
解答:解:设线段PQ上任意一点M(x,y),
且令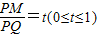 ,又P(2,-3),Q(3,2),
,又P(2,-3),Q(3,2),
则x=(1-t)2+3t=2+t,y=(1-t)(-3)+t•2=-3+5t,
将x和y代入直线ax+y+2=0得:a(2+t)+(-3+5t)+2=0,
解得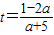 ,
,
由0≤t≤1得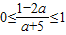 ,
,
解得: ,
,
故答案为:[- ,
, ]
]
点评:此题考查学生掌握两直线交点的意义,以及定比分点的公式.设出线段PQ任一点的坐标及定比t,找出t的范围是解得本题的关键.
解答:解:设线段PQ上任意一点M(x,y),
且令
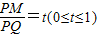 ,又P(2,-3),Q(3,2),
,又P(2,-3),Q(3,2),则x=(1-t)2+3t=2+t,y=(1-t)(-3)+t•2=-3+5t,
将x和y代入直线ax+y+2=0得:a(2+t)+(-3+5t)+2=0,
解得
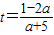 ,
,由0≤t≤1得
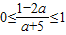 ,
,解得:
 ,
,故答案为:[-
 ,
, ]
]点评:此题考查学生掌握两直线交点的意义,以及定比分点的公式.设出线段PQ任一点的坐标及定比t,找出t的范围是解得本题的关键.

练习册系列答案
相关题目
 ;
; );
); 不可能表示椭圆.
不可能表示椭圆.