题目内容
已知点 的最小值是( )
的最小值是( )A.3
B.-3
C.

D.
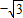
【答案】分析:利用三角换元,再利用辅助角公式,结合条件a2+b2≤3,即可得到结论.
解答:解:由题意设x=acosα,y=bsinα,则 x+y=acosα+bsinα=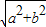 sin(α+θ)≥-
sin(α+θ)≥-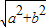
∵a2+b2≤3
∴x+y≥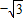
∴x+y最小值为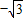
故选D.
点评:本题考查求最小值,解题的关键是利用三角换元,再利用辅助角公式求解.
解答:解:由题意设x=acosα,y=bsinα,则 x+y=acosα+bsinα=
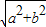 sin(α+θ)≥-
sin(α+θ)≥-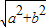
∵a2+b2≤3
∴x+y≥
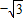
∴x+y最小值为
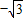
故选D.
点评:本题考查求最小值,解题的关键是利用三角换元,再利用辅助角公式求解.

练习册系列答案
相关题目
 是曲线
是曲线 上任意一点,则点
上任意一点,则点 的距离的最小值是
.
的距离的最小值是
.
 的最小值是
.
的最小值是
. 内接于圆
内接于圆 ,
, ,直线
,直线 切
切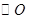 于点
于点 ,
, 交
交 于点
于点 .若
.若 则
则 的长为 .
的长为 .
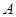 是曲线
是曲线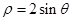 上任意一点,则点
上任意一点,则点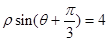 的距离的最小值是
.
的距离的最小值是
.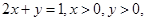
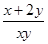 的最小值是
.
的最小值是
.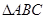 内接于圆
内接于圆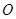 ,
,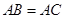 ,直线
,直线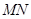 切
切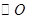 于点
于点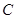 ,
,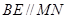 交
交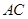 于点
于点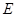 .若
.若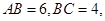 则
则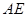 的长为 .
的长为 .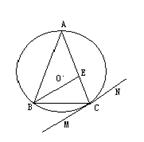
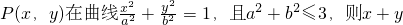 的最小值是
的最小值是
