题目内容
如图,在等腰△ABC中,AB=AC,底边上的高AD=10 cm,腰AC上的高BE=12 cm.(1)求证:![]() ;
;
(2)求△ABC的周长.
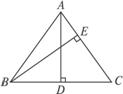
思路点拨:易证得△ADC∽△BEC,所以![]() ,关键是作等量代换:AB=AC,BC=2BD.第(2)问的证明充分利用第(1)问的结论,通过线段之间的关系构造方程求解.
,关键是作等量代换:AB=AC,BC=2BD.第(2)问的证明充分利用第(1)问的结论,通过线段之间的关系构造方程求解.
(1)证明:
在△ADC和△BEC中,
∵∠ADC=∠BEC=90°,∠C=∠C,
∴△ADC∽△BEC.
∴![]() =
=![]() =
=![]() =
=![]() .
.
∵AD是等腰△ABC底边的高线,
∴BC=2BD.
又AB=AC,∴![]() =
=![]() =
=![]() .
.
∴![]() .
.
(2)解:设BD=x,则AB=![]() x,
x,
在Rt△ABD中,∠ADB=90°.
根据勾股定理,得AB2=BD2+AD2.
∴(![]() x)2+x2=102.解得x=7.5.
x)2+x2=102.解得x=7.5.
∵BC=2x=15,AB=AC=![]() x=12.5,
x=12.5,
∴△ABC的周长为40 cm.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量| AB |
| AC |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
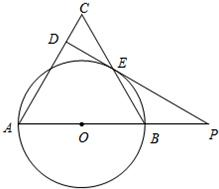 14、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
14、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由. 如图,在等腰△ABC中,
如图,在等腰△ABC中, 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量 如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.