题目内容
已知函数 .
.
⑴ 设 .试证明
.试证明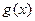 在区间
在区间  内是增函数;
内是增函数;
⑵ 若存在唯一实数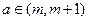 使得
使得 成立,求正整数
成立,求正整数 的值;
的值;
⑶ 若 时,
时, 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.
 .
.⑴ 设
 .试证明
.试证明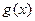 在区间
在区间  内是增函数;
内是增函数;⑵ 若存在唯一实数
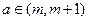 使得
使得 成立,求正整数
成立,求正整数 的值;
的值;⑶ 若
 时,
时, 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.(1)证明见解析
(2) .
.
(3)正整数 的最大值为3.
的最大值为3.
(2)
 .
.(3)正整数
 的最大值为3.
的最大值为3.(1)因为 所以
所以 .
.
∴ , 则
, 则 , ∴
, ∴  在
在 内单调递增 .
内单调递增 .
解:(2) ∵ ,
, ,∴由(1)可得
,∴由(1)可得 在
在 内单调递增,
内单调递增,
即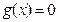 存在唯一根
存在唯一根 , ∴
, ∴  .
.
(3) 由 得
得 且
且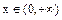 恒成立,由(2)知存在唯一实数
恒成立,由(2)知存在唯一实数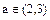 ,
,
使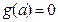 且当
且当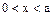 时,
时, ,∴
,∴  ,当
,当 时,
时,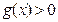 ,∴
,∴  .
.
∴ 当 时,
时,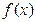 取得最小值
取得最小值 .
.
∵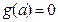 , ∴
, ∴ 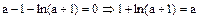 . 于是,
. 于是, ∵
∵ 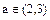 ,
,
∴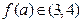 ∴
∴ ,故正整数
,故正整数 的最大值为3.
的最大值为3.
 所以
所以 .
.∴
 , 则
, 则 , ∴
, ∴  在
在 内单调递增 .
内单调递增 .解:(2) ∵
 ,
, ,∴由(1)可得
,∴由(1)可得 在
在 内单调递增,
内单调递增,即
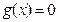 存在唯一根
存在唯一根 , ∴
, ∴  .
.(3) 由
 得
得 且
且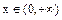 恒成立,由(2)知存在唯一实数
恒成立,由(2)知存在唯一实数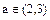 ,
,使
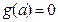 且当
且当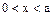 时,
时, ,∴
,∴  ,当
,当 时,
时,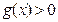 ,∴
,∴  .
.∴ 当
 时,
时,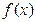 取得最小值
取得最小值 .
. ∵
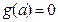 , ∴
, ∴ 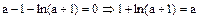 . 于是,
. 于是, ∵
∵ 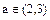 ,
,∴
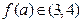 ∴
∴ ,故正整数
,故正整数 的最大值为3.
的最大值为3.
练习册系列答案
相关题目

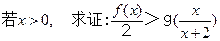
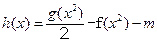 恰有四个不同的零点?若存在求出的m范围;若不存在,说明理由。
恰有四个不同的零点?若存在求出的m范围;若不存在,说明理由。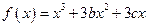 在两个极值点
在两个极值点 ,且
,且 。
。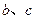 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 的区域;
的区域;

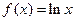 ,
,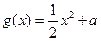 (
(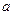 为常数),若直线
为常数),若直线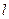 与
与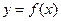 和
和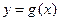 的图象都相切,且
的图象都相切,且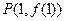 . (1)求直线
. (1)求直线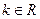 时,讨论关于
时,讨论关于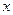 的方程
的方程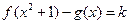 的实数解的个数.
的实数解的个数.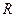 上的函数
上的函数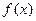 满足
满足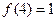 ,
,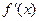 为
为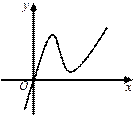
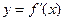 的图像如右图所示,
的图像如右图所示,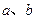 满足
满足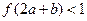 ,则
,则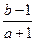 的取值范围是 .
的取值范围是 .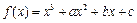 在
在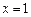 和
和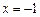 时取极值,且
时取极值,且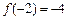 .
.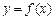 的表达式;
的表达式;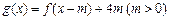 在区间
在区间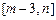 上的值域为
上的值域为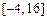 ,试求
,试求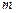 、n应满足的条件。
、n应满足的条件。 ,
, ,函数
,函数 的图象与
的图象与 轴的交点也在函数
轴的交点也在函数 的图象上,且在此点有公共切线.
的图象上,且在此点有公共切线. 、
、 的值;
的值; 的大小.
的大小.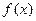 在点
在点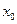 处可导,则函数
处可导,则函数