Question

【题目】已知函数f（x）=ax+ +c是奇函数，且满足f（1）= ，f（2）= ．
（1）求a，b，c的值；
（2）试判断函数f（x）在区间（0， ）上的单调性并证明．

Answer 1

【答案】
（1）解：∵f（﹣x）=﹣f（x）∴c=0，

∵ ，∴ ，

∴ ；

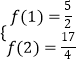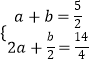（2）解：∵由（1）问可得f（x）=2x+ ，

∴f（x）在区间（0，0.5）上是单调递减的；

证明：设任意的两个实数0＜x1＜x2＜ ，

∵f（x1）﹣f（x2）=2（x1﹣x2）+ ﹣ =2（x1﹣x2）+ = ，

又∵0＜x1＜x2＜ ，

∴x1﹣x2＜0，0＜x1x2＜ ，1﹣4x1x2＞0，

f（x1）﹣f（x2）＞0，

∴f（x）在区间（0，0.5）上是单调递减的

【解析】（1）由函数是奇函数得到c=0，再利用题中的2个等式求出a、b的值．（2）区间（0， ）上任取2个自变量x1、x2 ， 将对应的函数值作差、变形到因式积的形式，判断符号，依据单调性的定义做出结论．
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较，以及对函数奇偶性的性质的理解，了解在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．