题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若![]() 在区间
在区间![]() 上恰有两个零点,求
上恰有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求出![]() ,利用导数的几何意义求切线斜率为
,利用导数的几何意义求切线斜率为![]() ,根据点斜式可得切线方程;(2)利用导数求出函数的极大值和极小值,利用
,根据点斜式可得切线方程;(2)利用导数求出函数的极大值和极小值,利用![]() 在区间
在区间![]() 上恰有两个零点列不等式组,求解不等式组即可求
上恰有两个零点列不等式组,求解不等式组即可求![]() 的取值范围.
的取值范围.
试题解析:(1)由已知得![]() ,
,
若![]() 时,有
时,有![]() ,
, ![]() ,
,
∴在![]() 处的切线方程为:
处的切线方程为: ![]() ,化简得
,化简得![]() .
.
(2)由(1)知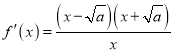 ,
,
因为![]() 且
且![]() ,令
,令![]() ,得
,得![]()
所以当![]() 时,有
时,有![]() ,则
,则![]() 是函数
是函数![]() 的单调递减区间;、
的单调递减区间;、
当![]() 时,有
时,有![]() ,则
,则![]() 是函数
是函数![]() 的单调递增区间. 9分
的单调递增区间. 9分
若![]() 在区间
在区间![]() 上恰有两个零点,只需
上恰有两个零点,只需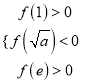 ,即
,即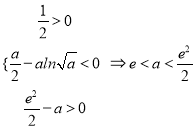 ,
,
所以当![]() 时,
时, ![]() 在区间
在区间![]() 上恰有两个零点.
上恰有两个零点.
【方法点晴】本题主要考查利用导数求曲线切线以及利用导数研究函数零点问题,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目